kingwinner
- 1,266
- 0
1) A vector form of Green's theorem states that under certain conditions,
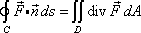
where n is the unit[/color] outward normal to the curve C and D is the region enclosed by C
[Now, my question is: must n be a unit vector? Why or why not?]
2) A "regular region" is a compact set S in Rn that is the closure of its interior. Equivalently[/color], a compact set S in Rn is a regular region if every neighborhood of every point on the boundary of S contains points in the interior of S
[I don't understand at all why these are equivalent. Can somebody please explain?]
Thanks a lot!
where n is the unit[/color] outward normal to the curve C and D is the region enclosed by C
[Now, my question is: must n be a unit vector? Why or why not?]
2) A "regular region" is a compact set S in Rn that is the closure of its interior. Equivalently[/color], a compact set S in Rn is a regular region if every neighborhood of every point on the boundary of S contains points in the interior of S
[I don't understand at all why these are equivalent. Can somebody please explain?]
Thanks a lot!
Attachments
Last edited: