Gyrocompass motion: Zero torque in the free axis

In summary: Well depending on what R is meant to be, you can also say: R x F is zero because the angle between R and F is 90° .
  • #1
RicardoMP
49
2
Hi!
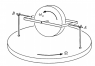
At the moment I'm studying rigid body motion, more specifically, the gyrocompass. As you can see in the attached picture (Introduction to Mechanics -Kleppner-Kolenkow-Chap.7), the gyrocompass rotates about the z axis and the spin angular momentum is reoriented towards the z axis, creating a angular momentum along the AB axis. As I've read, the pivots at A and B allow the system to swing freely about the y-axis (which is along AB), so there can be no torque along the y axis. Why is that? Why is the torque along any free axis zero? I know that there are a couple of contributions to torque along the y axis, for example, the change of direction of the spin angular momentum. Why must the sum of all these contributions be zero? My objective is to understand intuitively this concept so any time I'm faced with such an axis, I immediately assume that the torque along it is zero.
Sorry for the long post and thank you in advance!
 

Attachments

  • gyrocompass.PNG
    gyrocompass.PNG
    13.4 KB · Views: 645
Physics news on Phys.org
  • #2
RicardoMP said:
As I've read, the pivots at A and B allow the system to swing freely about the y-axis (which is along AB), so there can be no torque along the y axis. Why is that?
Look at the definition of torque, if an applied force passes through an axis, then it produces no torque around that axis. If the forks A & B are frictionless, can they apply any force to the cylindrical axle, that doesn't pass right through it's axis?
 
  • Like
Likes RicardoMP
  • #3
A.T. said:
Look at the definition of torque, if an applied force passes through an axis, then it produces no torque around that axis. If the forks A & B are frictionless, can they apply any force to the cylindrical axle, that doesn't pass right through it's axis?
Oh! Indeed! It is that simple. And so, the sum of all contributions to the torque along that axis equals the cross product R x F, in this case is zero, since the angle between R and F is zero.
Thank you!.
 
  • #4
RicardoMP said:
the cross product R x F, in this case is zero, since the angle between R and F is zero.
R x F is zero because R is zero, in this case.
 
  • #5
Ah yes, of course! My bad!
Thank you! :)
 
  • #6
RicardoMP said:
Ah yes, of course! My bad!
Thank you! :)
Well depending on what R is meant to be, you can also say: R x F is zero because the angle between R and F is 180° .
 

Related to Gyrocompass motion: Zero torque in the free axis

What is a gyrocompass and how does it work?

A gyrocompass is a type of compass that uses a spinning gyroscope to find true north. It works by utilizing the principle of gyroscopic precession, which is the tendency of a spinning object to resist changes in its orientation.

What is the significance of zero torque in the free axis of a gyrocompass?

Zero torque in the free axis of a gyrocompass means that the gyroscope is aligned with the earth's axis of rotation, allowing it to accurately determine true north. This is important because it ensures that the compass is not affected by external forces and remains stable, providing reliable navigation information.

How is zero torque achieved in the free axis of a gyrocompass?

Zero torque is achieved by suspending the gyroscope in a gimbal system, which allows it to freely rotate in all directions. The gimbal system is designed in such a way that the torque from the earth's rotation is cancelled out, resulting in zero torque in the free axis of the gyrocompass.

What factors can affect the zero torque in the free axis of a gyrocompass?

External forces such as magnetic fields, vibrations, and changes in temperature can affect the zero torque in the free axis of a gyrocompass. It is important to regularly calibrate and maintain the compass to ensure accurate readings.

What are the main applications of gyrocompasses?

Gyrocompasses are commonly used in marine navigation, aviation, and space exploration. They are also used in various scientific instruments such as seismometers and telescopes to maintain stability and accuracy.

Similar threads

I Why is there no torque along this axis?
    • Mechanics
Replies
2
Views
727
I Rotation about two axes and angular momentum
    • Mechanics
Replies
3
Views
924
Ball hits a pivoting rod, what torque changes the angular momentum of the ball?
    • Mechanics
Replies
14
Views
1K
I Conservation of angular momentum during collisions
    • Mechanics
Replies
3
Views
1K
Torque, angular momentum and a fixed axis-of-symmetry requirement
    • Mechanics
Replies
1
Views
793
Conceptual questions about Angular Momentum Conservation and torque
    • Mechanics
Replies
2
Views
1K
I Torque required to prevent precession
    • Classical Physics
Replies
2
Views
880
Force acting during rotating a disc
    • Mechanics
Replies
3
Views
3K
Angular acceleration in rigid body rotation due to a torque
    • Mechanics
Replies
1
Views
1K
Precession - why does the rotational axis change as L changes?
    • Mechanics
Replies
8
Views
1K

Hot Threads

Recent Insights

Back
Top