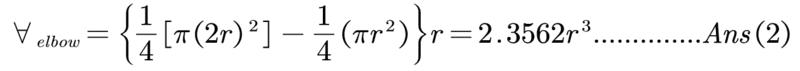SUMMARY
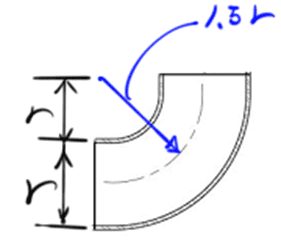
The discussion centers on calculating the volume of an elbow using integral calculus. The correct formula for the area of the circular cross-section is established as π(r/2)², leading to a volume of (3/16)π²r³ when integrated. The confusion arose from differing interpretations of the diameter and radius in the calculations. Ultimately, the resolution confirms that the volume of the elbow is accurately represented as 2.3562r³, consistent with the book's findings.
PREREQUISITES
- Integral calculus, specifically for volume calculations
- Understanding of circular cross-sections and their areas
- Familiarity with LaTeX for mathematical expressions
- Basic geometry, particularly regarding diameters and radii
NEXT STEPS
- Study the application of integrals in calculating volumes of irregular shapes
- Learn about the derivation of volume formulas for cylindrical and conical shapes
- Explore advanced calculus techniques, including triple integrals
- Practice using LaTeX for formatting mathematical equations
USEFUL FOR
Students and professionals in engineering, mathematics, and physics who are involved in fluid dynamics or structural analysis, particularly those needing to calculate volumes of complex shapes like elbows.