firavia
- 136
- 0
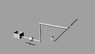
if we have a pipe system like in the figure below where a pump exist in the system in order to deliver 200 gpm of water from the tank "A". we need to deliver 150 gpm from "C" and 50 gpm from "D" usually we use the pipe flow chart of william hazen in order to size each pipe according to its flow from the chart we get the head loss per 100 feet of each pipe and finaly we calculate the head of the pump according to the path that have the bigger head loss.
my question is : in the problem below if we apply bernoulli equation between point "A,the top of the tank " and point "C" and between point "A" and point "D" and ignoring the dynamic energy effet cause it is small we get the head loss between these 2 paths are equal , but if we use william hazen equation and putting for each path a flow rate we get different head losses ,is there a contradiction ??
A-C bernoulli equation : 0 pressure + 0 velocity =HEAD LOSS THROUGH THE PATH -hEAD OF PUMP +Height between the top of the tank and point C
so the head loss through the path ABC is equal to head of pump + heaight between top of the tank and point C
now :
A-D bernoulli equation we will get the same Head loss .
but using william hazen equation each path has different head loss.
is there a contradiction or not ?
my question is : in the problem below if we apply bernoulli equation between point "A,the top of the tank " and point "C" and between point "A" and point "D" and ignoring the dynamic energy effet cause it is small we get the head loss between these 2 paths are equal , but if we use william hazen equation and putting for each path a flow rate we get different head losses ,is there a contradiction ??
A-C bernoulli equation : 0 pressure + 0 velocity =HEAD LOSS THROUGH THE PATH -hEAD OF PUMP +Height between the top of the tank and point C
so the head loss through the path ABC is equal to head of pump + heaight between top of the tank and point C
now :
A-D bernoulli equation we will get the same Head loss .
but using william hazen equation each path has different head loss.
is there a contradiction or not ?