Jweck002
- 7
- 0
- TL;DR
- Finding interior wall Temperature through a Multi Layer Cylinder knowing only exterior temp
Hello,
I am a Mechanical Engineer a little out of practice on Heat transfer. I am trying to solve this problem. It must be solvable but i have yet to find right equations online.
I have a multi Layer Cylinder made up of C350 marraging Steel,Zinc Alloy-12 , then 6061 Aluminum T6. All that is known is the temperature of the steel and of course the parameters & material properties of each metal. The temperature is over a time also. Outside surface starts 70 F @ 0 seconds and goes 180 F @ 25 s, 200 F @ 40s, 225F @ 45s, 250F @ 50s, 280 @ 60s.
I was looking for conductive heat transfer but all formulas i found need Q (heat flux). Which i don't believe i have. Please help.
Material properties:
C350 :
denisty : 0.292 lb/in^3
conductivity: k = 25.3 W/mK @ 20C
ZA-12:
density: 0.218 lb/in3
Conductivity: k = 110 W/m-K
Al 6061 T6:
Density: 0.0975 lb/in³
Conductivity: k= 167 W/m-k
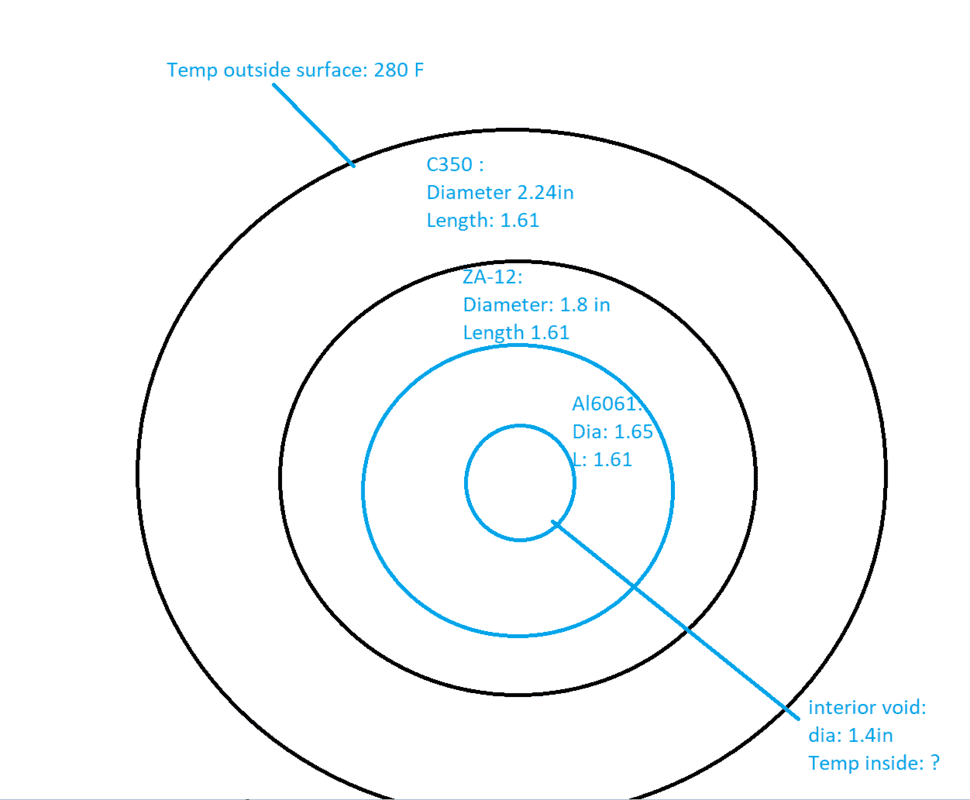
I am a Mechanical Engineer a little out of practice on Heat transfer. I am trying to solve this problem. It must be solvable but i have yet to find right equations online.
I have a multi Layer Cylinder made up of C350 marraging Steel,Zinc Alloy-12 , then 6061 Aluminum T6. All that is known is the temperature of the steel and of course the parameters & material properties of each metal. The temperature is over a time also. Outside surface starts 70 F @ 0 seconds and goes 180 F @ 25 s, 200 F @ 40s, 225F @ 45s, 250F @ 50s, 280 @ 60s.
I was looking for conductive heat transfer but all formulas i found need Q (heat flux). Which i don't believe i have. Please help.
Material properties:
C350 :
denisty : 0.292 lb/in^3
conductivity: k = 25.3 W/mK @ 20C
ZA-12:
density: 0.218 lb/in3
Conductivity: k = 110 W/m-K
Al 6061 T6:
Density: 0.0975 lb/in³
Conductivity: k= 167 W/m-k