Scronin267
- 17
- 0
Homework Statement
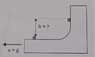
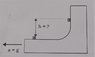
A block in the shape of a quarter circle moves at constant acceleration across the floor. At some moment a small block of mass m, which is at rest with respect to the floor, is placed atop the horizontal part of the large block. There is no friction in this problem. Assuming the small block does not fly off the large block, what is the greatest altitude increase it will achieve? What will happen after this height is obtained?
Homework Equations
potential energy U = mgh
kinetic energy T = 1/2mv^2
langrangian L = T-U, ∂L/∂q=d/dt ∂L/∂q'
The Attempt at a Solution
I do not know how to handle the kinetic energy of the large block... because we don't know the initial speed. I am also not sure if the lagrange approach is correct, but finding the forces along the path seems overly tedious. Can someone point me in the right direction? Should I be looking at momentum instead.
Last edited by a moderator: