Help me resolve this apparent paradox

[raxp]

This is the third time I try posting, and the first time after having written an Introduction. I hope it will work this time.

Imagine we have a cuboid of mass $M$ and height $2 r$ that slides without friction on a horizontal surface. It is accelerated by a line or rod that is connected to the axle of a wheel of mass $m$ (homogeneously distributed) and radius $r$. A rope or something similar is also connected to the wheel axle and a constant force $f$ is applied through it perfectly parallel to the ground. The entire system accelerates as a result and at any given moment, its velocity is $v$. See the figure below.

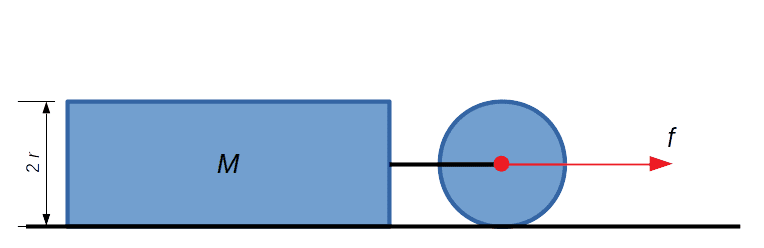
The kinetic energy of the system is $$E = \frac 1 2 M v^2 + \frac 1 2 m v^2 + \frac 1 2 (I + m r^2) \omega^2$$ where $I = \frac 1 2 m r^2$ is the moment of inertia of the wheel around its center and $\omega$ is its angular velocity; the extra term $m r^2$ comes from the parallel axis theorem since the wheel rotates around its lower perimeter and not its center. Now, since the wheel rolls without slipping, $v = r \omega$ and the kinetic energy reduces to a function of the single variable $v$ alone: $$E = \frac 1 2 (M + \frac 5 4 m) v^2$$

The person pulling the system performs work $f d$ where $d = \int v \mathrm d t$ is the total displacement. The power of this work, work per unit time, is hence $f v$ and all of this is converted into kinetic energy of the system, hence the equation $$\frac {\mathrm d E} {\mathrm d t} = (M + \frac 5 4 m) v a = f v$$ where $a$ is the linear acceleration. Assuming $v \neq 0$, we may solve this equation for $a$ to obtain Newton's second law with an effective mass: $$a = \frac f {M + \frac 5 4 m}$$.

Now consider the case where the attached rope is connected not to the wheel axle but to a point on the wheel perimeter. At a given moment, the situation is as depicted below.

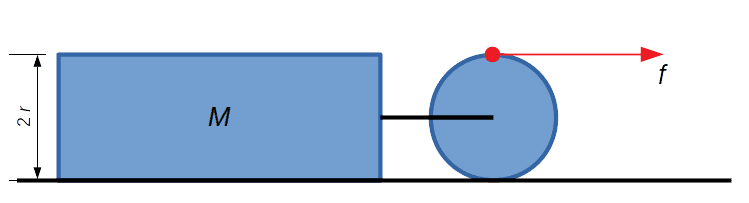
The work performed per unit time is now greater, since the top of the wheel is moving at a speed $2 v$, meaning that the power produced is now $2 f v$. Carrying out the same derivation as before, we obtain $$a = \frac {2 f} {M + \frac 5 4 m}$$ but this expression is independent of $r$, so that in the limit $r \to 0$ we have two different expressions for the induced acceleration, even though the point of application of the force is the same in both cases!

Where lies the error?

 

[Halc]

we obtain $$a = \frac {2 f} {M + \frac 5 4 m}$$ but this expression is independent of $r$, so that in the limit $r \to 0$ we have two different expressions for the induced acceleration, even though the point of application of the force is the same in both cases!

Where lies the error?

The expression is indeed not a function of r, so the limit of any constant expression as some irrelevant variable approaches anything is still the constant expression. At r=0, you're attaching the string to the edge of a point, which makes no sense, but if you could wind an infinitely thin rope around a point, it would still give you twice the work for a given force relative to just attaching the string to the point and not winding it around.

 

[raxp]

The expression is indeed not a function of r, so the limit of any constant expression as some irrelevant variable approaches anything is still the constant expression. At r=0, you're attaching the string to the edge of a point, which makes no sense, but if you could wind an infinitely thin rope around a point, it would still give you twice the work for a given force relative to just attaching the string to the point and not winding it around.

OK. And I take it the analogous explanation for the case where $M \to \infty$ and/or $m \to 0$? Introducing a massless wheel of vanishing radius before the mass $M$ will double the acceleration (essentially double the force)? The result is only counterintuitive, not paradoxical?

 

[Filip Larsen]

the wheel rotates around its lower perimeter and not its center

I don't understand why you say and model with this? Clearly, a homogeneous wheel rolling on a flat surface must rotate around its geometric center, which in this case is also its center of mass. Imagine the wheel is tied to a post (coming down from the ceiling) with a string and it is the floor that is accelerated horizontally under the wheel until the string force is F, would you still think the wheel rotates around the surface contact point?

 

[jbriggs444]

the extra term $mr^2$ comes from the parallel axis theorem since the wheel rotates around its lower perimeter and not its center.

You are double-dipping here.

If you want to be able to add the energy from linear motion together with the energy from rotational motion, you should be adding the energy from the linear motion of the center of mass together with the energy from the rotation of the object about its center of mass.

If choose you use the instantaneous center of rotation approach instead, then the entire motion of a rotating object at an instant is in captured by its rotation. There is no separate linear motion.

Edit: Let us try both approaches to see if they deliver the same result. If what I am saying holds water, they certainly should do so.

Approach number 1. Add kinetic energy from motion of center of mass to kinetic energy from rotation about the center of mass.$$KE=\frac{1}{2}mv^2 + \frac{1}{2}I \omega^2$$
Approach number 2. Take kinetic energy from rotation about center of mass and use parallel axis theorem to get kinetic energy from rotation about the instantaneous center of rotation.$$KE=\frac{1}{2}(I + mr^2)\omega^2$$At first glance, the two look different. But wait a bit, $v=\omega r$. If we make that substitution in the first formula, we get $$KE=\frac{1}{2}mr^2\omega^2 + \frac{1}{2}I \omega^2$$ which matches the second formula nicely.

 

[raxp]

I don't understand why you say and model with this? Clearly, a homogeneous wheel rolling on a flat surface must rotate around its geometric center, which in this case is also its center of mass. Imagine the wheel is tied to a post (coming down from the ceiling) with a string and it is the floor that is accelerated horizontally under the wheel until the string force is F, would you still think the wheel rotates around the surface contact point?

It depends on the reference frame. If we take the reference fram to be comoving with the floor, then yes. See below, however.

You are double-dipping here.

If you want to be able to add the energy from linear motion together with the energy from rotational motion, you should be adding the energy from the linear motion of the center of mass together with the energy from the rotation of the object about its center of mass.

If choose you use the instantaneous center of rotation approach instead, then the entire motion of a rotating object at an instant is in captured by its rotation. There is no separate linear motion.

Edit: Let us try both approaches to see if they deliver the same result. If what I am saying holds water, they certainly should do so.

Approach number 1. Add kinetic energy from motion of center of mass to kinetic energy from rotation about the center of mass.$$KE=\frac{1}{2}mv^2 + \frac{1}{2}I \omega^2$$
Approach number 2. Take kinetic energy from rotation about center of mass and use parallel axis theorem to get kinetic energy from rotation about the instantaneous center of rotation.$$KE=\frac{1}{2}(I + mr^2)\omega^2$$At first glance, the two look different. But wait a bit, $v=\omega r$. If we make that substitution in the first formula, we get $$KE=\frac{1}{2}mr^2\omega^2 + \frac{1}{2}I \omega^2$$ which matches the second formula nicely.

Yes, thank you. In other words $$E = \frac 1 2 (M + \frac 3 4 m) v^2$$ in the original post. As for the paradox, however, it still remains. In particular, if we let $r, m \to 0$ as per my second post above, we have a very peculiar situation.

 

[jbriggs444]

As for the paradox, however, it still remains. In particular, if we let r,m→0 as per my second post above, we have a very peculiar situation.

Extracting a limit tells you what happens as the wheel gets smaller and smaller but still remains a wheel.
Looking at the situation at the limit tells you what happens if there is no wheel.

 

[raxp]

Extracting a limit tells you what happens as the wheel gets smaller and smaller but still remains a wheel.
Looking at the situation at the limit tells you what happens if there is no wheel.

Yes, but the paradox is the following in this case:

You have before you a large weight, and even though its underside is lubricated, its inertia is simply too large for you to make an appreciable change to its velocity. You then add a small wheel (small $m r^2$) to the configuration, increasing the total mass (by $m$) and inertia of the system, but this simple increase of the mass of the system counterintuitively (or maybe paradoxically) leads the same efforts to almost twice the acceleration of the total system.

 

[jbriggs444]

Yes, but the paradox is the following in this case:

You have before you a large weight, and even though its underside is lubricated, its inertia is simply too large for you to make an appreciable change to its velocity. You then add a small wheel (small $m r^2$) to the configuration, increasing the total mass (by $m$) and inertia of the system, but this simple increase of the mass of the system counterintuitively (or maybe paradoxically) leads the same efforts to almost twice the acceleration of the total system.

Because you have twice the force. The force from you forward on the wheel plus the force of the ground forward on the wheel.

Two for one mechanical advantage still works, no matter how small the lever. But you do have to have the lever.

 

[raxp]

Because you have twice the force. The force from you forward on the wheel plus the force of the ground forward on the wheel.

Two for one mechanical advantage still works, no matter how small the lever. But you do have to have the lever.

I would love for this explanation to be correct (and it was my initial conclusion), but I have it on good authority that the frictional force from the ground for a single wheel when a force is applied parallel to the ground at the top as in my second case is zero, and that the ground friction force only contributes when the applied force is oblique or opposite to the direction of motion.

This is the vexing thing that I have been trying to understand since.

 

[jbriggs444]

from the ground for a single wheel when a force is applied parallel to the ground at the top as in my second case is zero, and that the ground friction force only contributes when the applied force is oblique or opposite to the direction of motion.

It depends on the situation. Is the frictional force from the ground on your tires zero when you press the accelerator in your car? Or the brakes?

For an ideal (massless and free from rolling resistance) free-wheeling (not driven and not being braked) wheel, the fore and aft frictional force from the ground is zero, yes. But we have a driven wheel here.

 

[Lnewqban]

I can't see any paradox.
If the same magnitude of force is applied for both cases, the second arrangement is providing double power (energy by unit of time) into the system.

This seems to be the same case of pushing a disabled car on a horizontal road.
There are two practical ways to do it by hand:
1) You can push on the trunk, applying force F along distance d to produce work W in time t.
2) 1) You can push on the top of a tire, applying force F/2 along distance 2d (regarding your hands) to produce work W in time t.

No matter how small or big the diameter of the tire is, the magnitude of F in case 2 will always be half the magnitude of F in case 1.
As the work on the car in time t is the same in both cases, its covered distance, linear and rotational accelerations and final velocity will be exactly the same.

 

[raxp]

It depends on the situation. Is the frictional force from the ground on your tires zero when you press the accelerator in your car? Or the brakes?

For an ideal (massless and free from rolling resistance) free-wheeling (not driven and not being braked) wheel, the fore and aft frictional force from the ground is zero, yes. But we have a driven wheel here.

Here is what I have been told of the frictional force, when a torque with net linear force is applied to the wheel. The green arrow represents the frictional force.

Is this wrong?

 

[raxp]

I can't see any paradox.
If the same magnitude of force is applied for both cases, the second arrangement is providing double power (energy by unit of time) into the system.

This seems to be the same case of pushing a disabled car on a horizontal road.
There are two practical ways to do it by hand:
1) You can push on the trunk, applying force F along distance d to produce work W in time t.
2) 1) You can push on the top of a tire, applying force F/2 along distance 2d (regarding your hands) to produce work W in time t.

No matter how small or big the diameter of the tire is, the magnitude of F in case 2 will always be half the magnitude of F in case 1.
As the work on the car in time t is the same in both cases, its covered distance, linear and rotational accelerations and final velocity will be exactly the same.

Well, the paradox must be apparent after all. The thing is, you speak here in terms of energy and work and I agree, it is hard to see any paradox then.

When, however, expressed dynamically in terms of the acceleration, you obtain Newton's second law with an effective mass that is smaller when the wheel is added (provided it is sufficiently light) to the assembly. For someone merely looking at the applied force on the system and the acceleration of the center-of-mass, it may seem paradoxical that adding mass to the system leads to an apparent reduction of the same in terms of linear inertia.

 

[jbriggs444]

Here is what I have been told of the frictional force, when a torque with net linear force is applied to the wheel. The green arrow represents the frictional force.
View attachment 300534
Is this wrong?

It is incomplete. No load vector is depicted at the hub.

I am not certain whether a uniform free-floating disc is a shape that leaves its lower rim stationary when subjected to a tangential force on its top rim. No matter. A negligibly massive uniform disk with a load applied to its center does not leave its lower rim stationary when a tangential force is applied to its upper rim.

 

[jbriggs444]

For someone merely looking at the applied force on the system and the acceleration of the center-of-mass, it may seem paradoxical that adding mass to the system leads to an apparent reduction of the same in terms of linear inertia.

Imagine the improvement in acceleration one could garner if, instead of attaching a simple pulley to the front, one attached a block and tackle.

 

[raxp]

Imagine the improvement in acceleration one could garner if, instead of attaching a simple pulley to the front, one attached a block and tackle.

No, the block and tackle are stationary and not part of the system.

 

[raxp]

It is incomplete. No load vector is depicted at the hub.

I am not certain whether a uniform free-floating disc is a shape that leaves its lower rim stationary when subjected to a tangential force on its top rim. No matter. A negligibly massive uniform disk with a load applied to its center does not leave its lower rim stationary when a tangential force is applied to its upper rim.

I don't quite follow. You are saying that taking into account the effect of gravity, there must be a forward frictional force in the left-most force diagram?

 

[jbriggs444]

I don't quite follow. You are saying that taking into account the effect of gravity, there must be a forward frictional force in the left-most force diagram?

I am saying that the left-most force diagram is incomplete. You do not show the force from the big block that is being pulled by the wheel.

 

[raxp]

I am saying that the left-most force diagram is incomplete. You do not show the force from the big block that is being pulled by the wheel.

No, that's true. That's a force that is equal to Ma. Including this load will increase the frictional force in the forward direction, such that in the left-most diagram, the frictional force is $f$?

 

[jbriggs444]

No, that's true. That's a force that is equal to Ma. Including this load will increase the frictional force in the forward direction, such that in the left-most diagram, the frictional force is $f$?

The force that is equal to $Ma$ is nowhere depicted on any of the four pictures.

In the leftmost diagram and assuming that the wheel is of negligible mass compared to $M$, yes, the rightward frictional force of floor on the wheel bottom is equal to the rightward applied force $f$ on the top of the wheel. The total of those two forces is approximately $2f$