- #1
Juanda
- 292
- 100
- TL;DR Summary
- I realized I can't confidently draw the FBD of a wheel coming to a stop.
Simple question. Let's say a solid cylinder has an initial speed ##v_o## and it's rotating on infinitely hard ground without air resistance.
The cylinder will come to a stop eventually. There are two sources of friction.
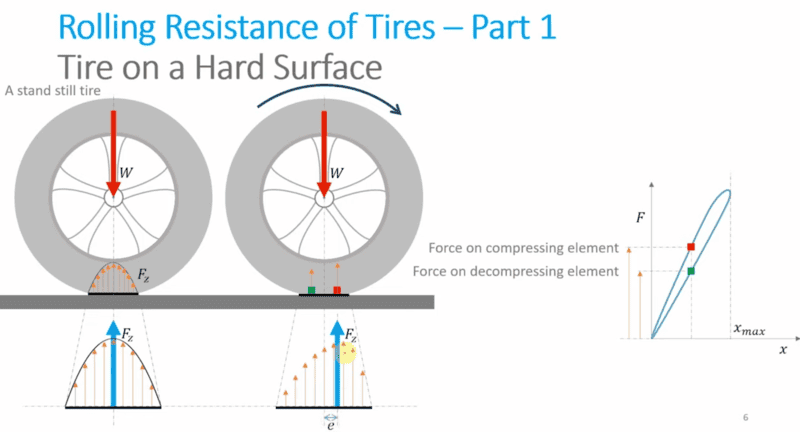 That picture is from this video. My concern is that, although he doesn't mention it directly, he's assuming the wheel has no angular acceleration to obtain a formula for the rolling resistance.
That picture is from this video. My concern is that, although he doesn't mention it directly, he's assuming the wheel has no angular acceleration to obtain a formula for the rolling resistance.
So I'm trying to draw a FBD of the cylinder and make the equations work but I'd love to have confirmation of my thought process to make sure it's right.
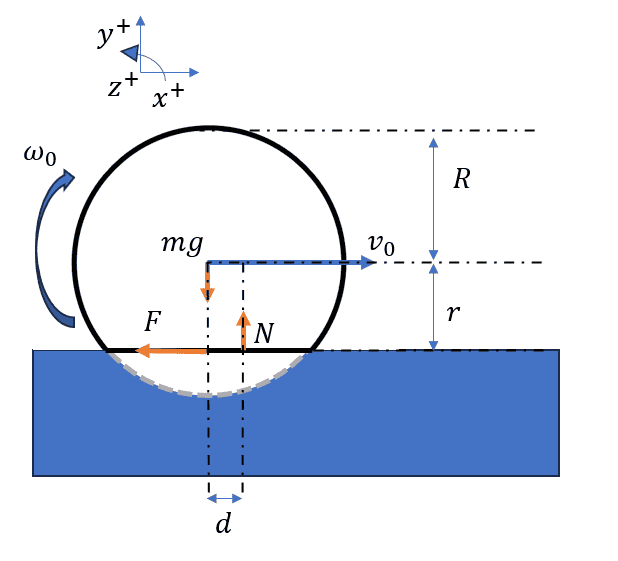
Vertical forces. The normal force must necessarly exist and be equal to the weight because there is no vertical acceleration.
$$-mg+N=0 \rightarrow N = mg$$
Horizontal forces. The force ##F## must exist because we know the acceleration in ##x## of the body will decrease with time. I'll consider the value to be initially unknown.
$$-F=ma_x$$
Torques. Due to the hysteresis, the normal force is not alligned with the weight. Let's assume for now that ##d## is known since we should be able to approximate it from the properties of the material. Also, due to the deformation of the wheel, the force ##F## has a smaller leverage ##r## instead of ##R##.
$$-Fr+Nd=I \alpha$$
Where ##I \approx \frac{1}{2}mR^2##
Mechanical link. The rotation of the wheel and the horizontal displacements are related. A positive turn of the wheel moves it in the negative horizontal direction so there will be a minus sign in there. I have doubts about using ##r## or ##R##. I believe ##r## is more accurate.
$$\alpha r \approx -a_x$$
We know everything from the first equation so we are left with 3 equations and 3 unknowns ##F, a_x, \alpha##. This is solvable.
After clearing the unknowns I get the following.
$$\alpha = \frac{Nd}{I+mr^2}$$
$$F = \frac{Ndmr}{I+mr^2}$$
$$a_x = - \frac{Ndr}{I+mr^2}$$
From that, I can get the linear and angular velocities and how they change with time so I can obtain the power being lost. However, I feel I should be able to obtain the same result using ##P=Fv## or ##P= \tau \omega## but I wouldn't even know which force or torque to input in those equations.
To me, it feels like the approach is correct. However, it bothers me it looks so different when compared with the usual ##F_f= \mu N##. How would you solve a problem like this?
The cylinder will come to a stop eventually. There are two sources of friction.
- Since the wheel/cylinder is deformed at the contact patch, there is some sliding friction that will consume energy.
- Materials are not really elastic so hysteresis happens. Especially with rubber-like materials typically used for tires. Due to the viscoelastic behavior of the wheel, the rotational energy of the wheel will be transformed into heat because of the internal friction. I believe this to be the main friction source since the sliding friction could not even happen if the wheel is sticky and can deform enough.
So I'm trying to draw a FBD of the cylinder and make the equations work but I'd love to have confirmation of my thought process to make sure it's right.
Vertical forces. The normal force must necessarly exist and be equal to the weight because there is no vertical acceleration.
$$-mg+N=0 \rightarrow N = mg$$
Horizontal forces. The force ##F## must exist because we know the acceleration in ##x## of the body will decrease with time. I'll consider the value to be initially unknown.
$$-F=ma_x$$
Torques. Due to the hysteresis, the normal force is not alligned with the weight. Let's assume for now that ##d## is known since we should be able to approximate it from the properties of the material. Also, due to the deformation of the wheel, the force ##F## has a smaller leverage ##r## instead of ##R##.
$$-Fr+Nd=I \alpha$$
Where ##I \approx \frac{1}{2}mR^2##
Mechanical link. The rotation of the wheel and the horizontal displacements are related. A positive turn of the wheel moves it in the negative horizontal direction so there will be a minus sign in there. I have doubts about using ##r## or ##R##. I believe ##r## is more accurate.
$$\alpha r \approx -a_x$$
We know everything from the first equation so we are left with 3 equations and 3 unknowns ##F, a_x, \alpha##. This is solvable.
After clearing the unknowns I get the following.
$$\alpha = \frac{Nd}{I+mr^2}$$
$$F = \frac{Ndmr}{I+mr^2}$$
$$a_x = - \frac{Ndr}{I+mr^2}$$
From that, I can get the linear and angular velocities and how they change with time so I can obtain the power being lost. However, I feel I should be able to obtain the same result using ##P=Fv## or ##P= \tau \omega## but I wouldn't even know which force or torque to input in those equations.
To me, it feels like the approach is correct. However, it bothers me it looks so different when compared with the usual ##F_f= \mu N##. How would you solve a problem like this?