- #1
HeZ
- 10
- 1
Hello all,
Semester has just started and i am dong a 4th year dynamics unit, so i am reviewing the previous years unit which was a pre-requisite for the unit i am currently doing. I have come across a rather difficult dynamics problem that was given as a challenge question at the beginning of last years course - one which i never managed to solve. It is really doing my head in and I am hoping someone here can help me with it?
It is as follows:
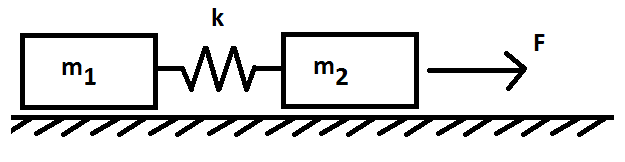
Two masses connected by a linear spring, constant k. A force is applied to mass m2.
There IS friction.
What is the minimum constant force F that will cause mass m1 to move?
I am assuming that the spring can be considered massless, as i have never been given a problem in which this was not the case, and a spring mass was not given.
And I forgot to indicate in the image that gravity acts downwards (perpendiculat to the surface), not that it matters.
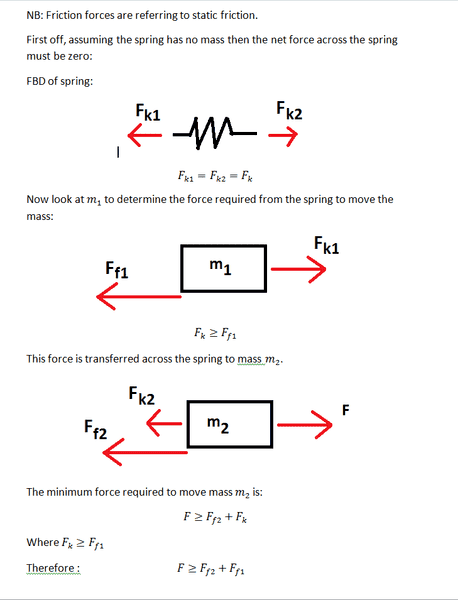
I tried many solutions, all of which I was told were wrong. Below is one of them, I will type more of them up later when i have some spare time if necessary.
Thanks in advance
Chris
Semester has just started and i am dong a 4th year dynamics unit, so i am reviewing the previous years unit which was a pre-requisite for the unit i am currently doing. I have come across a rather difficult dynamics problem that was given as a challenge question at the beginning of last years course - one which i never managed to solve. It is really doing my head in and I am hoping someone here can help me with it?
It is as follows:
Two masses connected by a linear spring, constant k. A force is applied to mass m2.
There IS friction.
What is the minimum constant force F that will cause mass m1 to move?
I am assuming that the spring can be considered massless, as i have never been given a problem in which this was not the case, and a spring mass was not given.
And I forgot to indicate in the image that gravity acts downwards (perpendiculat to the surface), not that it matters.
I tried many solutions, all of which I was told were wrong. Below is one of them, I will type more of them up later when i have some spare time if necessary.
Thanks in advance
Chris
