Help please with biocalculus question involving differentiation

[sarahjonester78]

Hi, I was just wondering how one would arrive at the answers to these questions. I have the solution for parts a and b, but not for part c.

Suppose that antibiotics are injected into a patient to treat a sinus infection. The antibiotics circulate in the blood, slowly diffusing into the sinus cavity while simultaneously being filtered out of the blood by the liver. A model for the concentration of the antibiotic in the sinus cavity as a function of time since the injection:

c(t) = [e^(−αt) − e^(−βt)]/ β − α
Where β > α > 0.

(a) At what time does c have its maximum value?
SOLUTION: t = [ln(α) − ln(β)] / α - β

I know that to be a maximum value the t would need to be solved with the use of: c¹(t)>0 , as well as the fact that natural log rules can be applied to this equation to make differentiation easier. But I have no idea how to get there and achieve the final answer.

(b) At what time does the inflection point occur?
SOLUTION: t = 2[ln(α) − ln(β)] / α - β

I do know that for a point of inflection c²(t)=0, as well as the fact that the same application of natural log rules would apply for this problem. But I don't know how to apply this for this problem.

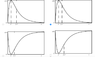
(c) what would the graph of c look like?
*attached picture shows options..
I did come to the conclusion that it has to be one of the top two graphs, but I don't know which one/why.

Any help would be much appreciated! :)

 

[NFuller]

I know that to be a maximum value the t would need to be solved with the use of: c1(t)>0 ,

I do know that for a point of inflection c2(t)=0, as well

Are you saying you don't know how to take the derivative? Have you taken calculus yet?

You need to show some attempt at the solution so we can see where you are stuck.

 

[sarahjonester78]

I know how to get the derivatives (see attached). But I don't know/understand what to do next. Also I have taken calculus.

 

[NFuller]

Your derivatives are not correct. The $e^{-\alpha t}$ term is missing.