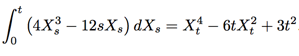Help solving/proofing an Integral Equation
- Context: MHB
- Thread starter cdbsmith
- Start date
Click For Summary
SUMMARY
This discussion focuses on proving the equality of both sides of the integral equation given by the expression $\displaystyle d(X_t^4 - 6tX_t^2 + 3t^2) = (4X_t^3 - 12tX_t)\, dX_t$. The proof utilizes Ito's lemma, where the function $f(t, x) = x^4 - 6tx^2 + 3t^2$ is differentiated to show that the differential form simplifies to the required equality. The key steps involve calculating the partial derivatives and applying the lemma correctly, confirming the equality holds under the assumption that $X_0 = 0$.
PREREQUISITES- Understanding of stochastic calculus and Ito's lemma
- Familiarity with differential equations and their applications
- Knowledge of partial derivatives and their computation
- Basic concepts of integral equations in mathematical analysis
- Study the applications of Ito's lemma in stochastic processes
- Explore advanced topics in stochastic calculus, such as stochastic differential equations
- Learn about the properties and applications of integral equations in mathematical modeling
- Review examples of proving equality in integral equations for deeper understanding
Mathematicians, students of stochastic calculus, and researchers working with integral equations and their proofs will benefit from this discussion.
Similar threads
- · Replies 6 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 1 ·
Graduate
Integral of squared univariate PDF
- · Replies 8 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 2 ·