Help -- Time Domain Power, Volt-Amperes in lagging circuit

[mdaugird]

Please find attached a spreadsheet trying to plot an inductive/resistive circuit in the time domain and show instantaneous power and Volt Amperes.
Logic tells me power can not go negative, but I am not sure my power plot is correct.
Can someone please review the spreadsheet and chart to tell me if I am doing anything wrong?
I divided the VA and Power by 100 just to make the curves fit the graph. If my equations are correct i will address the formatting and second y-axis scale. How do I

attach a spreadsheet?
http://www.daugird.com\Book1.xlsx

 

[berkeman]

Please find attached a spreadsheet trying to plot an inductive/resistive circuit in the time domain and show instantaneous power and Volt Amperes.
Logic tells me power can not go negative, but I am not sure my power plot is correct.
Can someone please review the spreadsheet and chart to tell me if I am doing anything wrong?
I divided the VA and Power by 100 just to make the curves fit the graph. If my equations are correct i will address the formatting and second y-axis scale. How do I View attachment 96150 attach a spreadsheet?
http://www.daugird.com\Book1.xlsx

Welcome to the PF.

If V(t) and I(t) are not in phase, then yes, there can be times when the instantaneous power goes negative.

 

[mdaugird]

how? I see VA going negative, but how can real power go negative?

 

[berkeman]

how? I see VA going negative, but how can real power go negative?

When the sinusoidal current and voltage waveforms are in phase, they have the same sign during the whole cycle, so the product is always positive.

When they are out of phase, for part of each cycle they will have opposite signs, and hence their product will be negative.

But you can probably see that already from your graphs. Are you asking *physically* what is going on? Since positive real instantaneous power represents power being consumed by the load, what do you think negative instantaneous power represents...?

 

[mdaugird]

The graph shows real power always being positive, I was just surprised it was exactly in phase with the voltage.
The VA in the graph follows your logic but not real power.
Negative power from passive components would seem to be impossible and that is why I responded the way I did.
I might be mis-reading your responses but all of your responses seem to relate to the VA curve, and my questions are pointed at Real Power dissipated.

 

[berkeman]

The graph shows real power always being positive, I was just surprised it was exactly in phase with the voltage.
The VA in the graph follows your logic but not real power.
Negative power from passive components would seem to be impossible and that is why I responded the way I did.
I might be mis-reading your responses but all of your responses seem to relate to the VA curve, and my questions are pointed at Real Power dissipated.

How are you calculating the graph of "real instantaneous power"? I could be wrong, but I believe that the real power is the time average of the instantaneous power. That's how you can have some negative values of the instantaneous power, but the average will still always be positive.

 

[anorlunda]

Instantaneous power V*I, has no real and imaginary components. Instantaneous power is real power. During one cycle without of phase V and I, it will become negative part of the time. If V and I are 180 degrees out of phase, it will be negative or zero the whole cycle.

If you are calculating instantaneous Real power as separate from volt-amps, then I don't know what calculations you are doing. Can you elaborate?

 

[mdaugird]

is what I am using for time domain real power and VA is just v(t) * i(t)
is the spreadsheet accessible at the link? I couldn't attach it.

 

[berkeman]

View attachment 96151
is what I am using for time domain real power and VA is just v(t) * i(t)
is the spreadsheet accessible at the link? I couldn't attach it.

So you are artificially calculating a waveform that would be the real power, if V & I were in-phase...

In real life, you don't have that. You have V(t) and I(t), from which you can get the instantaneous power waveform, and you can calculate Irms and Vrms over a cycle. Using those values, you can calculate the power factor PF = Average Real Power / (Vrms*Irms). The Average Real Power is the average of the instantaneous power waveform over one cycle.

https://en.wikipedia.org/wiki/Power_factor

From the Power Factor triangle, you can get the value of the "Real Power" and "Imaginary Power". Does that make more sense?

 

[jim hardy]

Simplify your thinking..

Does instantaneous power equal instantaneous volts X instantaneous amps ?
If not, what does it equal?

That formula in post 8 can not go negative. Where did it come from?

Anorlunda and Berkeman both nailed it. Study their comments.

 

[sophiecentaur]

my questions are pointed at Real Power dissipated.

You are making the wrong inference from what your results tell you.
The 'power' that you are seeing, represents the rate at which energy is being stored in and returned by the reactive components. At the end of each cycle, the net energy in the reactances is zero and so the net power 'dissipated' in them is zero.

 

[Averagesupernova]

Strangely enough I didn't encounter anything that plotted voltage, current and reactive power all at the same time in school. At least not at first. I recall having a hard time wrapping my head around how power can be returned to the source at first. When I saw the graph for the first time it all made sense. It certainly is counter intuitive for the current to go 'the wrong direction' in part of the AC cycle but indeed that is what happens.

 

[berkeman]

Yeah, I also was not exposed to this in a clear way in school, or even in my work afterward. But recently I've been tasked with designing and coding a "metrology" application that publishes power used by loads connected to my device. It's been interesting learning about how to deal with low power factor devices...

 

[sophiecentaur]

Yeah, I also was not exposed to this in a clear way in school, or even in my work afterward.

That doesn't surprise me, actually. It falls in a crack between Power Engineering (see all the threads about Reactive Power, showing it's a new and unexplained idea for many people) and 'ordinary Electronics', where the flow of energy in reactive circuits is treated in a different way and V.I isn't a particularly relevant quantity.
Looking at a graph is a bit like looking at a painting or reading a poem; everyone sees it slightly differently and spots a different set of details. They do their best but lecturers can't always be expected to take people through all the pathways in a relationship between quantities.

 

[jim hardy]

When it clicked for me was when i encountered my first electronic wattmeter. An analog multiplier IC does real time analog multiplication of instantaneous volts X instantaneous amps then averages the result.

this one uses the AD633 multiplier
http://mysite.du.edu/~etuttle/electron/elect64.htm

http://www.analog.com/media/en/trai...ndbooks/ADI_Multiplier_Applications_Guide.pdf

http://www.analog.com/media/en/technical-documentation/data-sheets/AD633.pdf

Arithmetic tells us
The average of the products is different from the product of the averages , and it's different from the product of the RMS's .

The average of the (instantaneous)products is watts
The product of the RMS's is volt-amps

 

[mdaugird]

thank you. I am hearing that the v(t) x i(t) is the power and that the reactive component is what is allowing it to go negative.
When I run the spreadsheet with unit power factor it results in an all positive curve for VA.
so looking at the watt meeter, how does a commercial meter have a VA and KW reading that is different on an "instantaneous" basis.
it sounds like i need 1 cycle to average over to separate the 2 values.

 

[sophiecentaur]

how does a commercial meter have a VA and KW reading that is different on an "instantaneous" basis.

I don't think a commercial meter shows its instantaneous answers. Surely it gives a mean value for the set of V.I values it calculates.

 

[anorlunda]

Reactive power is defined as an average oover integer multiples of whole cycles, $\frac{N}{60}$ o$\frac{N}{50}$ seconds. Instantaneously, it doesn't exist. However that average can change with time, and that is what a meter shows you dynamically.

 

[jim hardy]

so looking at the watt meter, how does a commercial meter have a VA and KW reading that is different on an "instantaneous" basis.

Let's take a look at a wattmeter.

The 330k and 20 k resistors divide tha 120V down to a manageable size signal for volts,
and the 10 ohm resistor gives a second signal that's proportional to current.
The 633 does an instant by instant multiplication of those two signals.
The rightmost opamp averages that product.

http://electronicdesign.com/energy/what-s-difference-between-watts-and-volt-amperes][/PLAIN]
The concept for calculating the real power for ac circuits is straightforward, though performing the calculation is much more difficult. To get the power in watts, you need to know the instantaneous voltage with time, v(t), and the instantaneous current with time, i(t). When you multiply these together, you get the instantaneous power with time, p(t).

Since this instantaneous power is changing over time, we need to get an average value, so we integrate the power over a period of time and divide by the time period to get the average. That gives us the watts dissipated by the device in a circuit with voltage v(t) across it and current i(t) through it for the period of time evaluated. Assuming that the voltage and current are both periodic waveforms of period T, the strict mathematical way to express the power calculation for a periodic waveform of period T is:

So while this may be easy to visualize, it is not easy to calculate. Even the measurement of real power in watts for ac circuits requires specialized equipment (a wattmeter) because the voltage and current waveforms must be measured over a precise period of time, the measurements must be simultaneous, and the average must be calculated over the measurement time period. A standard multimeter can’t make this type of power measurement.

now
if volts = Vsin(ωt) and amps is Asin(ωt)
the product is VAsin²(ωt) = (1-cos(2ωt) ) /2 note double frequency
and notice that value is never negative , the math says so. I can believe that math ,even if only because volts and amps have same sign at every instant.

Okay, so just to make things interesting let's shift current by 90 degrees so it's all wattless reactive power
volts = Vsin(ωt) and amps is Acos(ωt)
the product is VAsin(ωt)cos(ωt) = ( VA sin(2ωt) ) / 2 , again note double frequency
and notice this time math says it's not offset so averages zero.
Intuitively, volts and amps have opposite signs half the time so the products will be half negative and half positive probably averaging zero.

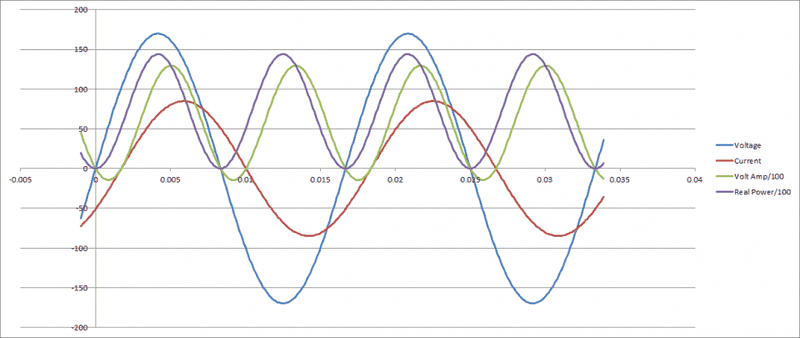
Now let's take a look at the two inputs to the analog wattmeter for the second case
(mainly because i couldn't find waveforms for the first case)

here's the waveforms you'd see with an oscilloscope
what they call "power" is instantaneous volts X instantaneous amps, output of the multiplier, observe it's double frequency and has no offset
the straight line is averaged power signal.

Hmmm. The wattmeter reports zero watts for a pure reactive load

If you replaced the reactive load with a resistive one
power = (1-cos(2ωt) ) /2
that blue double frequency power wave would shift up to reflect the 1 in that equation
and it'd shift over to realign the zero points
and the wattmeter would report its nonzero average
it has no choice , Mother Nature made math that way

usually if math says something is so Mother Nature won't disagree.
I love electronics because it's so close to math.
I'm awkward at math , but that circuit i can visualize and work in my head. (I think my mild autism helps...)

old jim

edit - oops i notice my waveforms start with voltage at peak instead of current at peak . Would have been better for me to have chosen Volts as cosine and Amps as sine
mea culpa i seem always to get things backward and it's frustrating
but i do stand behind the math.
I hope dear readers will forgive my clumsiness.