Help with Friction Forces: Box resting on a board on a frictionless surface

AI Thread Summary
The discussion centers on understanding the forces acting on a box resting on a board on a frictionless surface. The original poster is confused about why their calculation of the minimum force needed to move the box is incorrect, despite knowing the correct answer involves the combined mass of both objects. Key points include the realization that the force of static friction must be considered as a net force acting on the box, and that the force required to move the box must account for both masses to prevent them from moving together. The conversation emphasizes the importance of recognizing the limits of static friction and the need to apply sufficient force to overcome it. Ultimately, the clarification highlights the complexities of friction forces in systems with multiple masses.
alomari
Messages
2
Reaction score
0
Homework Statement
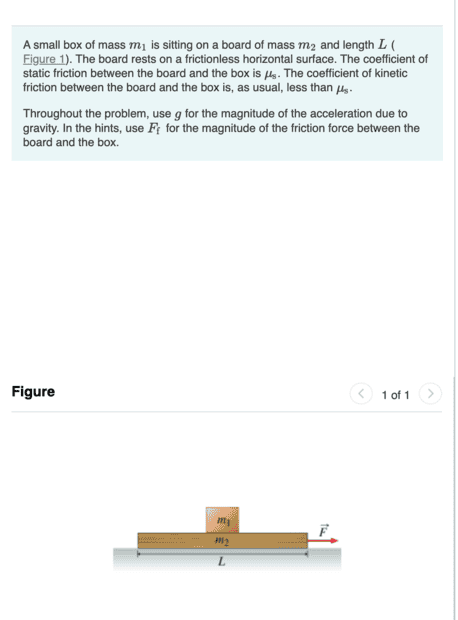
A small box of mass m1 is sitting on a board of mass m2 and length L (Figure 1). The board rests on a frictionless horizontal surface. The coefficient of static friction between the board and the box is μs. The coefficient of kinetic friction between the board and the box is, as usual, less than μs.

Throughout the problem, use g for the magnitude of the acceleration due to gravity. In the hints, use Ff for the magnitude of the friction force between the board and the box.

Figure1 of 1
The figure shows a box of mass m 1 lying on a board of mass m 2 and length L. The board lies on a horizontal surface. Force F acts to the right on the board.
Part A
Find Fmin, the constant force with the least magnitude that must be applied to the board in order to pull the board out from under the the box (which will then fall off of the opposite end of the board).Express your answer in terms of some or all of the variables μs, m1, m2, g, and L. Do not include Ff in your answer.
Relevant Equations
Static friction force : Fs = μs N
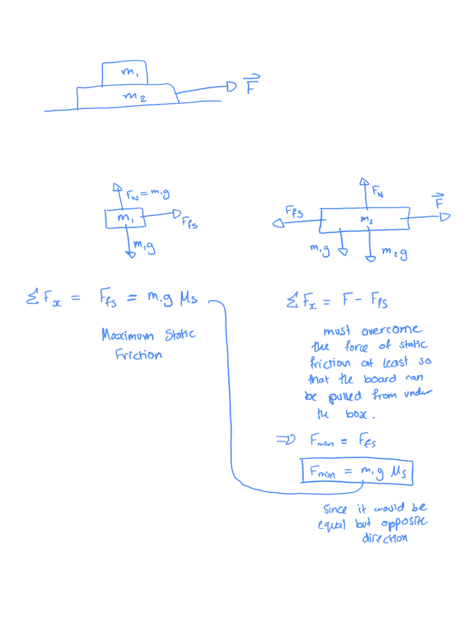
Hello, I'm struggling understanding why my answer to this question is incorrect. I know the right answer, but why is this way wrong? I have attached my solution and would really appreciate the help.
Thank you!
1714477955027.png
1714477965529.png

1714477995859.png
 

Attachments

Physics news on Phys.org
Imagine that the mass ##m_2## is huge, say, the mass of Earth. According to your answer, pulling the Earth with the force ##F_{min}=m_1 g \mu_s## would move it out from under the box ##m_1## sitting on it...
 
Hill said:
Imagine that the mass ##m_2## is huge, say, the mass of Earth. According to your answer, pulling the Earth with the force ##F_{min}=m_1 g \mu_s## would move it out from under the box ##m_1## sitting on it...
I understand, and the answer (m1 + m2)g μs makes logical sense, but I don't understand why my working is not right? The force of friction acting on the box on top would be the same as the force of friction acting on the box on the bottom, and wouldn't we just have to apply a minimum force of the same magnitude to overcome it? Am I missing a force vector here?
 
What will be the accelerations of the two bodies if ##F=m_1\mu_s g##?
 
alomari said:
Am I missing a force vector here?
No, you are not missing a force, but
alomari said:
we just have to apply a minimum force of the same magnitude to overcome it
is incorrect. We rather need to prevent them from moving together.
 
alomari said:
I understand, and the answer (m1 + m2)g μs makes logical sense, but I don't understand why my working is not right? The force of friction acting on the box on top would be the same as the force of friction acting on the box on the bottom, and wouldn't we just have to apply a minimum force of the same magnitude to overcome it? Am I missing a force vector here?
Start by considering that the force of static friction ##F_f## is the net force on ##m_1## in the horizontal direction. Remember that the force of static friction has an upper limit that it cannot exceed.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »
Thread 'Minimum mass of a block'

Thread 'Minimum mass of a block'

Here we know that if block B is going to move up or just be at the verge of moving up ##Mg \sin \theta ## will act downwards and maximum static friction will act downwards ## \mu Mg \cos \theta ## Now what im confused by is how will we know " how quickly" block B reaches its maximum static friction value without any numbers, the suggested solution says that when block A is at its maximum extension, then block B will start to move up but with a certain set of values couldn't block A reach...
View full post »

Similar threads

Is it friction or tension acting on the person hanging on a rope?
Replies
4
Views
1K
Understanding Free Body Diagrams: Explaining the Forces on a Compressed Board
Replies
7
Views
2K
Relation between Friction, Velocity, and Acceleration
Replies
16
Views
972
Free body Diagram of a Plank resting on two Cylinders
Replies
14
Views
3K
Why are tension and friction in the same direction?
Replies
6
Views
3K
Potential Mistake in Free-Body Diagram
Replies
5
Views
2K
Direction of friction on two stacked boxes
Replies
9
Views
4K
Solving Free-Body Diagrams for Moving Nuts on Rods: Tips and Techniques
Replies
9
Views
2K
Box on treadmill connected to a spring
Replies
8
Views
1K
Finding Radial Force from Free Body Diagram
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top