Box on treadmill connected to a spring

[MigMRF]

Homework Statement

A box of mass m is placed on a treadmill. The box is connected to a stationary wall to the left via. a sping. The dynamic coeffecient of friction between the box and the treadmill is mu_k and the sping constant is k. The treadmill moves to the right. How far will it stretch the spring (assuming it is unstreched before we start)

Relevant Equations

Newtons laws, Energy conservation

First i show the sketch of the setup:

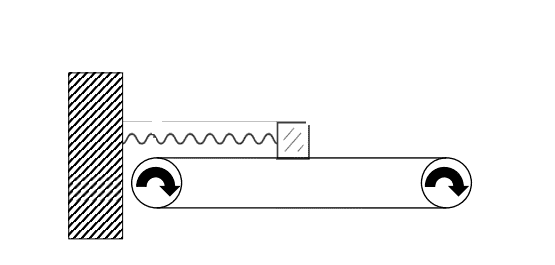
My first attempt was just to balance out the forces on the box. On the sketch below i have shown the situation where the spring is stretched distance L.

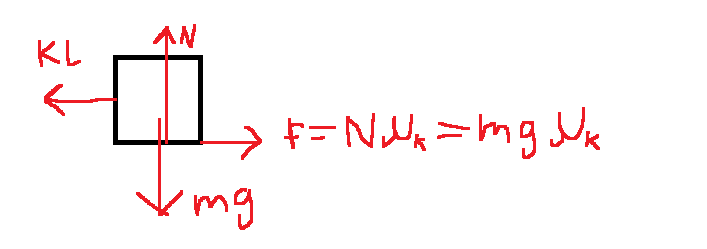
In this situation we get the equations:

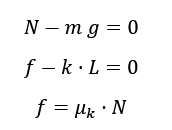
Which when solved leads to

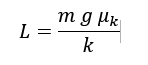
All good. I then looked at the proposed solution. Here they instead looked at the conservation of energy, saying that the work done by the friction should equal the stored potential energy of the spring:

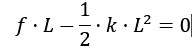
Which then leads to:

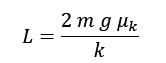
I can't really see why the two methods do not yield the same result and why my solution is incorrect. Any suggestions?

 

[anuttarasammyak]

Another $\frac{mg\mu_k}{k}$ was dissipated by friction to e.g. thermal energy, sonic energy.

 

[Doc Al]

All good. I then looked at the proposed solution. Here they instead looked at the conservation of energy, saying that the work done by the friction should equal the stored potential energy of the spring:
View attachment 331362
Which then leads to:
View attachment 331363
I can't really see why the two methods do not yield the same result and why my solution is incorrect. Any suggestions?

One problem in your "energy" approach is assuming that the friction force on the box equals $\mu_k mg$ from the start. But the friction force starts at zero, increasing as the spring stretches, until it reaches a maximum of $\mu_k mg$.

 

[nasu]

Up to the point where the two forces balance the friction is larger than the elastic force so the box accelerates. At the equilibrium point it has some speed and KE. So it keeps moving, until this KE is dissipated. The body oscillates around the equilibrium position you found yourself. Their answer is the maximum position.

 

[Doc Al]

Up to the point where the two forces balance the friction is larger than the elastic force so the box accelerates.

I suppose it depends on how the treadmill is moving, but the friction force will remain static -- and just what it needs to be to prevent the box from slipping -- until its max value is reached and the box has no choice but to start slipping.

 

[nasu]

You are right, it is static to start with if you start the teradmill after you put the box on it.
I was thinking that you put the box on the moving treadmill just because they provide only kinetic friction and it is also the simplest scenario, I believe.

 

[haruspex]

The question is not fully defined.

If we suppose the belt goes from rest instantaneously to a speed v then the box will slip immediately. The frictional force exerted by the belt is $\mu mg$, so long as the box has not reached speed v.
This will lead to SHM, as @nasu notes, but if $v<\mu g\sqrt{\frac mk}$ then at some point the box will reach speed v and the frictional force will decline to $kx$. The box will then continue at speed v until $kx=\mu mg$.

At one extreme, v is very small and the box quickly matches the belt speed. Assuming static and kinetic coefficients are the same, the maximum stretch is given by $kx=\mu mg$, as in your own solution.
At the other extreme, $v>\mu g\sqrt{\frac mk}$, the box reaches twice that distance

 

[kuruman]

How about ignoring how the block was started or whether is it oscillating and focus on the situation where the spring maintains a final fixed constant length. In the steady-state, the power dissipated as heat by friction is provided by the potential energy stored in the spring:$$\begin{align} & \frac{dU}{dt}=f_k v \nonumber \\
& kxv=\mu_k mgv \implies x=\frac{\mu_k mg}{k}. \nonumber \end{align}$$As @haruspex indcated, anything goes when one considers the transient behaviour.

 

[nasu]

Whatever powers the thread mill provides both the elastics energy stored in the spring and the energy dissipated, until the static regime is reached. Once the box is static, the elastic energy in the spring is constant. The energy dissipated by friction is provided by the treadmill's motor which is powered by electrical energy provided by whatever...