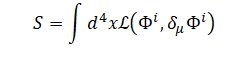Discussion Overview
The discussion revolves around integration conventions as presented in "Spacetime and Geometry" by Sean Carroll, specifically focusing on the notation used for integrals in classical field theory. Participants explore the implications of using different forms of integration notation.
Discussion Character
Main Points Raised
- One participant asks whether the integral can be expressed in terms of individual differentials (dx, dy, dz, dt) instead of the compact notation d4x.
- Another participant responds affirmatively, explaining that using d4x is often a matter of convenience and avoids emphasizing the order of integration. They also mention conditions under which iterated integrals are equivalent to integrals over regions, referencing Fubini's theorem.
- A third participant confirms their understanding and appreciation of the explanation provided.
- A fourth participant provides a link to a related discussion on the forum for further reference.
- The initial poster expresses satisfaction with the responses received.
Areas of Agreement / Disagreement
Participants generally agree on the convenience of using d4x for integration, but there is no explicit consensus on the necessity or implications of different notations.
Contextual Notes
The discussion does not address specific conditions under which the equivalence of integration forms holds, nor does it resolve the implications of using different notation in various contexts.