The only reason i have been asking this:
\int_a^b f(r(t)) |r'(t)|dt \neq \int_a^b \nabla f(r(t)) \cdot r'(t)dt
is because the formula given on the book say that they should be equal. However, as i try many examples; i never get the same answer. Here is some general proof i have been trying but never got far.
Let f(x,y)=f(x,y)
F = \nabla f(x,y)=<f_x, f_y>
Let Parametrization of Curve C:
r(t) = <g(t), h(t)>
r'(t) = <g'(t), h'(t)>
|r'(t)| = [g'(t)^2 + h'^2(t)]^\frac{1}{2}
\int_a^b f(r(t)) |r'(t)|dt = \int_a^b \nabla f(r(t)) \cdot r'(t)dt
\int_a^b f(g(t), h(t))[g'(t)^2 + h'(t)^2]^\frac{1}{2}dt = \int_a^b <f(_x, f_y> \cdot <g'(t), h'(t)>dt
\int_a^b f(g(t), h(t))[g'(t)^2 + h'(t)^2]^\frac{1}{2}dt = \int_a^b g'(t)f_x(g(t), h(t))+ h'(t)f_y(g(t), h(t))dtSince limits and variable of integration are the same then
f(g(t), h(t))[g'(t)^2 + h'(t)^2]^\frac{1}{2} = g'(t)f_x(g(t), h(t)) + h'(t)f_y(g(t), h(t))
But since i don't have any idea of what is going on inside those partial derivatives, i don't have a clue how to proceed.
Edit: In addition, the right hand side kind of looks like the product rule of a derivative.
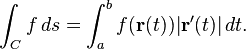 given a scalar function f. equation1
given a scalar function f. equation1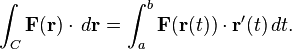 given a vector field F. equation2
given a vector field F. equation2