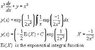Help with solving a first order linear and first order non-linear

In summary, the conversation discusses two different differential equations and the attempts made to solve them. The first equation leads to an unsolvable integral, while the second equation requires the use of a special function for a closed form solution. The use of an integrating factor is also mentioned, but it is not applicable in this case. The problem of expressing y(x) in terms of elementary functions is also brought up.
  • #1
Xyius
508
4
Here is an image of the first order linear differential equation and my attempt to solve it. It ends in an integral that can not be solved.

http://img831.imageshack.us/img831/9937/math1.gif

And here is an image of the first order non-linear differential equation and my attempt to solve it. This one leads to a non-separable differential equation after a substitution.

http://img215.imageshack.us/img215/4893/math2.gif

Any advise?
 
Last edited by a moderator:
Physics news on Phys.org
  • #2
You have:

[tex](1-y)dx+xydy=0[/tex]

You can find the [itex]1/M(M_y-N_x)[/itex] integrating factor for that.
 
  • #3
jackmell said:
You have:

[tex](1-y)dx+xydy=0[/tex]

You can find the [itex]1/M(M_y-N_x)[/itex] integrating factor for that.

The integrating factor isn't working. I was under the impression you can only use the integrating factor only when the two partials differ by a constant only, which they do not. :\
 
  • #4
Separable ODE :
 

Attachments

  • LambertW.JPG
    LambertW.JPG
    8.8 KB · Views: 432
  • #5
y(x) cannot be expressed in terms of a finite number of elementary functions. The closed form requires a special function :
 

Attachments

  • ExpIntegral.JPG
    ExpIntegral.JPG
    9.8 KB · Views: 350

FAQ: Help with solving a first order linear and first order non-linear

How do I solve a first order linear equation?

To solve a first order linear equation, you need to rearrange the equation into the form dy/dx = f(x). Then, you can use the method of separation of variables or an integrating factor to solve for y.

What is the difference between a first order linear and first order non-linear equation?

A first order linear equation has a variable raised to the first power and can be solved using standard mathematical techniques. A first order non-linear equation has a variable raised to a power other than one and usually requires more advanced methods to solve.

What is the purpose of solving a first order linear and non-linear equation?

Solving these types of equations is important in many fields of science and engineering. It allows us to model and predict the behavior of systems, such as population growth, chemical reactions, and electrical circuits.

What are some common techniques used to solve first order non-linear equations?

Some common techniques include substitution, separation of variables, and the use of integrating factors. Additionally, numerical methods such as Euler's method or the Runge-Kutta method can be used to approximate solutions.

Are there any real-world applications of first order linear and non-linear equations?

Yes, these types of equations are used in many real-world scenarios, such as predicting the spread of infectious diseases, modeling stock market trends, and designing control systems for robots and vehicles.

Similar threads

I Question about solving linear first order non-homogeneous ODEs
Replies
3
Views
2K
I Second order non-homogeneous linear ordinary differential equation
Replies
2
Views
2K
I Explanation of all "its linearly independent derivatives"
Replies
3
Views
2K
I How to do Magnus expansion for time-dependent companion matrix?
Replies
7
Views
941
I Solution:Second Order Linear Non-Homogenous ODEs in Physics
Replies
1
Views
2K
I Classification of First Order Linear Partial Differential Eq
Replies
1
Views
2K
I How do I solve this first order second degree differential equation?
Replies
7
Views
3K
I Fundamental matrix of a second order 2x2 system of ODEs
Replies
2
Views
2K
A Improper boundary in non-linear ODE (pseudospectral methods)
Replies
4
Views
1K
B First Order Non-Linear ODE (what method to use?)
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top