- #1
Rabscuttle
- 3
- 0
This isn't a homework problem or anything, If I don't think about the formula that I use, and just plug in numbers I get the right answer. But I feel like a robot doing so, and it bothers me.
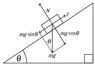
On a typical problem where a wedge sits on an inclines plane, I am given the angle of the slope in degrees And the Mass of the object. I draw my right triangle and using the old convention of making the height of the right triangle equal to "O" (for opposite) and the base equal to "A" (for adjacent) and the hypotaneus. "H"
I set my Y axis along the normal. and my X perpendicular. I assume that now my hypotenous represents Weight in the X direction since my "O" is Weight.
The formula for the Weight in the X direction is MG*SIN(theta) as it says in the book.
Using methods I know I get MG/SIN(theta)
I know how to get MG*SIN(theta), by drawing my triangle elsewhere. I just have no idea why they are different.
I'm not sure if I am being unclear, I wish I could upload a diagram.
Homework Statement
On a typical problem where a wedge sits on an inclines plane, I am given the angle of the slope in degrees And the Mass of the object. I draw my right triangle and using the old convention of making the height of the right triangle equal to "O" (for opposite) and the base equal to "A" (for adjacent) and the hypotaneus. "H"
I set my Y axis along the normal. and my X perpendicular. I assume that now my hypotenous represents Weight in the X direction since my "O" is Weight.
The formula for the Weight in the X direction is MG*SIN(theta) as it says in the book.
Using methods I know I get MG/SIN(theta)
I know how to get MG*SIN(theta), by drawing my triangle elsewhere. I just have no idea why they are different.
I'm not sure if I am being unclear, I wish I could upload a diagram.