Help with Venus Transit AU calculations

[YarnJunior]

Hello!

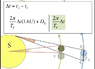
So I've been looking at making a decent calculation of the AU from the 2012 transit. As you can see from the first picture (Taken with the South Pole at the top), this is the method I'm using from the following video:



I use 2*(Pi)/Period of Earth to calculate the angular speed from two points. Afterwards, we multiply that by the change in time to get the angle. Multiplying that by the distance of the Earth from the sun gives us the arc length, which, added to the Diameter of the Earth, equals 2*(Pi)*Change in Time/Period of Venus. Rearranging this equation gives us the AU.

So I have a lot of questions. But please remember that I kinda had to dig a lot of information up myself and have very little experience with astronomy or astrophysics, so if you see something that makes absolutely no sense I apologize in advance. Anyways:

1. I'm not QUITE sure why we add the diameter of the Earth in this case? I know it's the distance between observations, but in this case we need the distance of the Earth between the two points of observation, not necessarily the diameter of the Earth, right?

2. What is the Change in Time exactly? I assume it's the difference between the time for external egress to external ingress for Observers A and the time for external egress to ingress for Observers B. This is usually a 5-13 minutes, right?

3. Where do we take these measurements? At which points on Earth do we need to record the transit for the needed data.? Other solutions I've seen take into account solar parallax, but, from my understanding, they are measured on the same longitude. In this case, we need to have measuring on the same latitudes with very different longitudes, right? Because the measurement is between the first people that see the transit and the last people that do. Sadly, I remembered that the Earth is inclined. So I'm not quite sure what to do at this case.

Anyways, that's basically it. I'm really sorry for the ignorance here but I am very new to this and am having a little bit of trouble understanding everything.

Thanks for the help!

 

[Bandersnatch]

Hello YarnJunior

The two observations you're making both measure the one moment when the limb of Venus first touches the limb of the Sun as the video shows at around 1:40.
Hence:

1. I'm not QUITE sure why we add the diameter of the Earth in this case? I know it's the distance between observations, but in this case we need the distance of the Earth between the two points of observation, not necessarily the diameter of the Earth, right?

You're making the two measurements on two opposite sides of the Earth. In the time between the measurements the Earth will have moved in orbit by the arc length $\frac{2\pi}{T_E} \Delta t$. On top of that distance, you've moved to the other side of the planet to make your second measurement, so you, the observer, have traveled more than just what the Earth did. You're farther from the point of your first measurement by one diameter of Earth.
Notice that for the case of calculations involving Venus as shown in the video, both measurements are for the same side of the planet (the lines of the triangle both touch the same side), so the distance does not include Venus' diameter.

2. What is the Change in Time exactly? I assume it's the difference between the time for external egress to external ingress for Observers A and the time for external egress to ingress for Observers B. This is usually a 5-13 minutes, right?

The difference is the difference between times at which you make the two measurements - one on the one side of the Earth, and the other sometime later on the other side of the Earth. Remember that the event of Venus touching the limb of the sun happens at different times for different observers. You're measuring this difference for the two selected observers at opposite sides of the planet.
This is the single instant of Venus touching the Sun's limb - the time for the planet to pass the limb does not concern you (if that's what you meant).

3. Where do we take these measurements? At which points on Earth do we need to record the transit for the needed data.? Other solutions I've seen take into account solar parallax, but, from my understanding, they are measured on the same longitude. In this case, we need to have measuring on the same latitudes with very different longitudes, right? Because the measurement is between the first people that see the transit and the last people that do. Sadly, I remembered that the Earth is inclined. So I'm not quite sure what to do at this case.

The measurements as depicted in the video should be taken from points where the ecliptic (Earth's orbital plane) bisects the globe of Earth. Only then you can be sure that the additional distance between the two observations is equal to the Earth's diameter.
These will be both lying on a line passing through the centre of the Earth. 31/05 is near the summer solstice, so the two points would be near the equator.

It is possible to make corrections for other latitudes and longitudes with some use of trigonometry, but that's more unnecessary work.
The two observations at the opposite sides of the Earth were chosen specifically to make things simpler.

 

[Gaz]

does Venus not bend light like the sun does? And what about Earth's effects on light does nothing like that have to be taken into account ?

 

[marcus]

Good question. there's a formula for the size of that effect, which depends on the mass. In the case of Earth and Venus the deflection angle would be too small to detect---to small to be taken into account. I'll try to find the formula. You could use it to see for yourself how small the angle would be.

As I recall the formula involves calculating a small distance r = 4GM/c^2
which would be about 6 kilometers for the sun.
And then the deflection angle, in radians, is something like r/R where R is how close to center the light ray passes.

But I should check that to make sure I'm not misremembering.

Yeah, that's right:
https://en.wikipedia.org/wiki/Gravi...tion_in_terms_of_space.E2.80.93time_curvature

You can check in the case of the earth, if M is mass of Earth and R is radius of Earth the angle would be too small to measure
When I paste this into google and press enter
4*G*mass of earth/c^2/radius of earth
Google comes back with
"((4 * G * mass of Earth) / (c^2)) / radius of Earth =
2.78122848 × 10-9"

It knows the Newton G and the mass of the Earth and the speed of light etc. so I don't have to look anything up, so the angle would be 3 billionths of a radian. too small to measure.
Light bending by the atmosphere would be significant, but not gravitational bending.