Highest probability of finding an electron

[PhoenixWright]

Hello.

I have found an exercise that reads: "The wave function of a one-electron atom is:

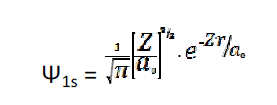[1s orbital, atom: Li²⁺ What will be the most likely distance to locate the electron?"

Solution of exercise is:

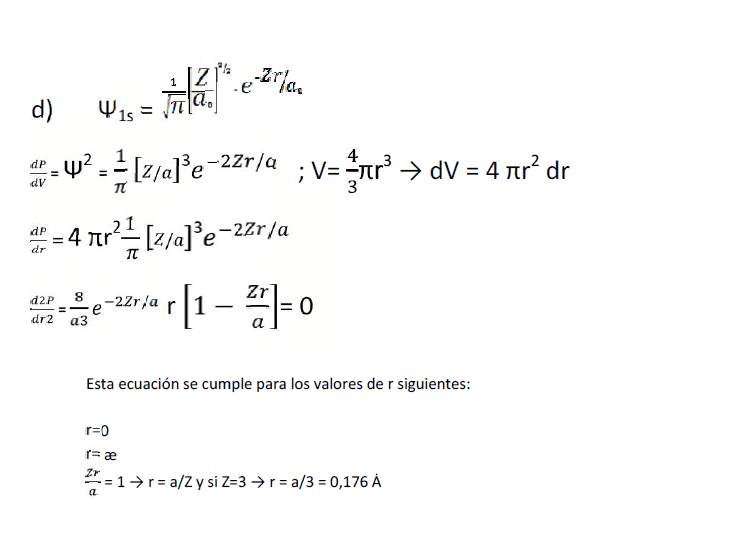
My question is: Why the square of the probability density is dP/dV, and therefore the volume formula is used?

I had always done this exercise by the square of the wave function, deriving the function and finding the maximum... I don't know why it's used the volume of a sphere here...

Thank you!

 

[blue_leaf77]

I will give a 1D example. An integral $P(x) = \int_{a}^x |\psi(x')|^2 dx'$ gives the probability of finding a particle between any constant $a$ and $x$, differentiating $P(x)$ with respect to $x$ gives $|\psi(x)|^2$.

 

[PhoenixWright]

Thank you!

Sorry, but I don't understand the relation between this:

I will give a 1D example. An integral $P(x) = \int_{a}^x |\psi(x')|^2 dx'$ gives the probability of finding a particle between any constant $a$ and $x$, differentiating $P(x)$ with respect to $x$ gives $|\psi(x)|^2$.

and the volume of the sphere... I had never done this type of exercise in this way, so I don't understand why this exercise is different...

I don't have advanced knowledge, since I'm starting...

Thanks!

 

[blue_leaf77]

I will give a 1D example. An integral $P(x) = \int_{a}^x |\psi(x')|^2 dx'$ gives the probability of finding a particle between any constant $a$ and $x$, differentiating $P(x)$ with respect to $x$ gives $|\psi(x)|^2$.

Define a function $F(x)$ such that
$$
|\psi(x)|^2 = \frac{d F(x)}{dx}
$$
So,
$$
\frac{d P(x)}{dx} = \frac{d}{dx} \int_{a}^x |\psi(x')|^2 dx' = \frac{d}{dx} (F(x) - F(a)) = \frac{dF(x)}{dx} = |\psi(x)|^2
$$
For 3D case, the logic may be slightly elaborate as it involves three variables but the intuition from 1D case can be directly applied. In the current problem, the radial probability $P(r)$ between a point $r'=a$ and $r$ is defined by
$$
P(r) = \int_a^r \int_0^{\pi} \int_0^{2\pi} |\psi_{1s}(r')|^2 r'^2 \sin \theta dr' d\theta d\phi = \int_a^r |\psi_{1s}(r')|^2 4\pi r'^2 dr'
$$
Taking derivative with respect to $r$
$$
\frac{d P(r)}{dr} = \frac{d}{dr}\int_a^r |\psi_{1s}(r')|^2 4\pi r'^2 dr' = |\psi_{1s}(r)|^2 4\pi r^2
$$

 

[PhoenixWright]

Thank you very much, blue_leaf77. Now I have understood correctly.

 

[vela]

Another way to look at it...

My question is: Why the square of the probability density is dP/dV, and therefore the volume formula is used?

The square of the modulus of the wave function is the probability density, i.e., $dP/dV = \| \psi(\vec{r}) \|^2$. This is one of the basic assumptions of quantum mechanics.

The probability $dP$ of finding the particle in an infinitesimal volume $dV$ around the point $(r, \theta, \phi)$ is given by
$$dP = \| \psi(r, \theta, \phi) \|^2\,dV = \| \psi(r, \theta, \phi) \|^2r^2\,dr\,d(\cos\theta)\,d\phi.$$ If you want the probability of finding the particle at a distance $r=r_0$, you have to sum over all possibilities meeting this criterion. That is, you need to integrate over the angles. Because the wave function is spherically symmetric, you end up with
$$dP_r = \int_0^{2\pi} \int_{-1}^1 \| \psi(r) \|^2r^2\,dr\,d(\cos\theta)\,d\phi = 4\pi r^2 \| \psi(r) \|^2\,dr.$$ In other words, the marginal probability density $f_r(r)$ is given by $f_r(r) = 4\pi r^2 \| \psi(r) \|^2$.

I had always done this exercise by the square of the wave function, derivingdifferentiating the function and finding the maximum... I don't know why it's used the volume of a sphere here.

 

[PhoenixWright]

Thank you, Vela. My questions have been clarified. It is always good to see two ways.