- #1
Dell
- 590
- 0
in the following question i am asked to whow that Y1 and Y2 are basic solutions to the homogeneous equations
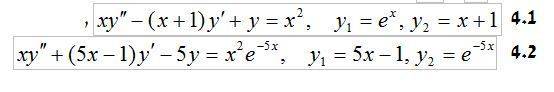
for 4.1)
y=ex=y' =y''
xy'' - (x+1)y' + y = x2
xex - (x+1)ex + ex = 0
none of these seem to work, what am i doing wrong?
for 4.1)
y=ex=y' =y''
xy'' - (x+1)y' + y = x2
xex - (x+1)ex + ex = 0
none of these seem to work, what am i doing wrong?