Discussion Overview
The discussion revolves around the mechanics of a ball bouncing on a surface, specifically examining how friction affects the normal force, bounce height, and bounce angle. Participants explore the implications of friction on the ball's motion, including the conversion of angular momentum and the relationship between horizontal and vertical velocities during the bounce.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- Some participants question how friction can lead to a larger normal force, noting that the normal force is typically dependent on vertical impulse, which they argue should remain constant across different scenarios.
- Others propose that the presence of friction allows for the conversion of angular momentum into deformation, potentially providing an additional boost to the ball's motion.
- It is suggested that the drawing in question may not indicate a higher maximum height but rather a higher bounce angle, which can be achieved by reducing horizontal velocity or increasing vertical velocity.
- One participant raises the question of whether a ball bouncing with friction can achieve a higher vertical velocity compared to a frictionless ball, considering the trade-off between linear and rotational kinetic energy.
- Another participant asserts that including the Earth in the system allows for conservation of angular and linear momentum, implying that no conservation law is violated in this context.
Areas of Agreement / Disagreement
Participants express differing views on the effects of friction on the normal force and the implications for bounce height and angle. There is no consensus on whether the frictional ball can achieve a higher vertical velocity than the frictionless ball, and the discussion remains unresolved.
Contextual Notes
Participants note that the interpretation of the drawing and the relationship between horizontal and vertical velocities are central to the discussion, with some assumptions about the system's closed nature being highlighted.
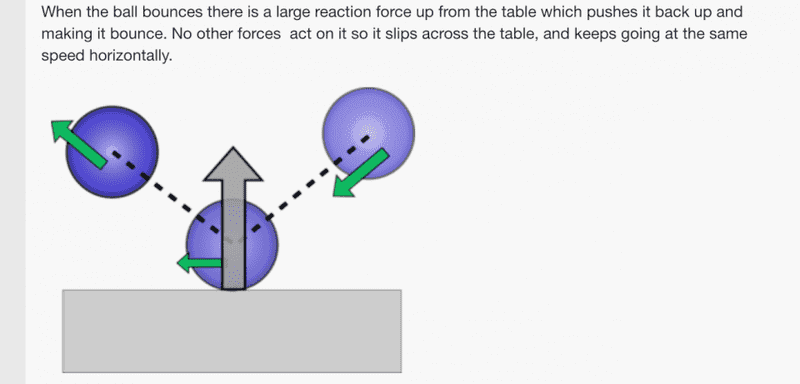Then is a case with friction
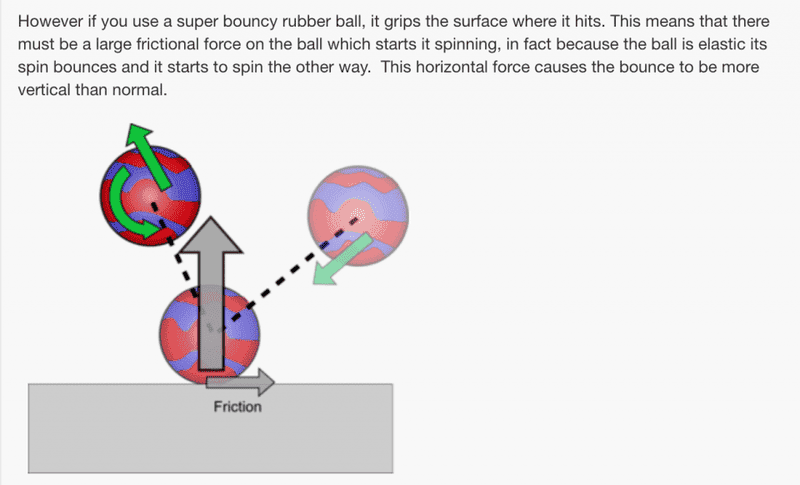Now what I don't understand is how is the presence of friction going to make the normal force larger than usual. The friction is dependent on the normal force, not the other way around. And the normal force is dependent on the vertical impulse, which should the same as the previous case, since the CM of the ball has the same final vertical velocity before impact.