How can generatrices be parallel to the y-axis?

[Adesh]

TL;DR

How can generatrices be parallel to the y-axis when the cross-section is perpendicular to the y-axis?

CONTEXT: We are finding the the buoyancy force on a boat which is upright in a still water (Fluid at rest) and the only gravity is acting as the external force. So, first we go for imaging a proper geometry of our boat.
See this figure :

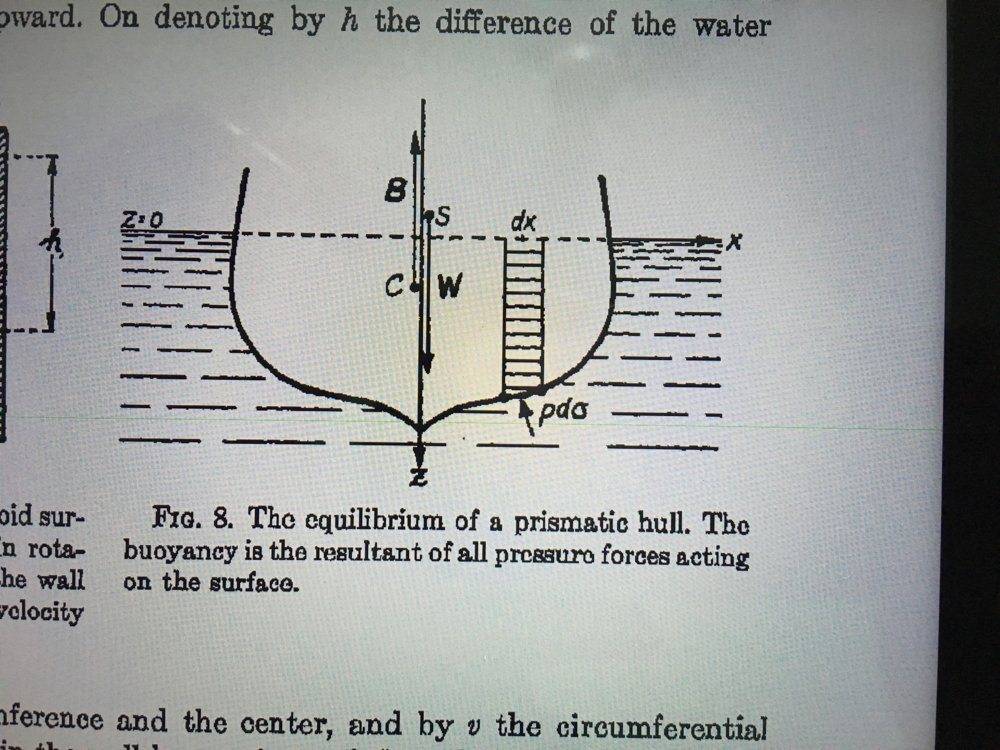
For this figure the book writes:
Fig 8 represents a cross-section normal to the longitudinal axis of the boat (positive y-axis forward). Let us think of the hull as the cylindrical surface with generatrices parallel to the y-axis.

I cannot understand what’s going on in the image. First the book writes that the displayed cross-section is perpendicular to the y-axis and then he writes that the generatrices is parallel to the y-axis. Because according to me generatrix is same as the cross-section, because Wikipedia says that a generatrix is something which when moved forms a complete figure.

So, if our main figure-to-be is cylinder (with axis as the y-axis) then our generatrix has to be a circle perpendicular to the y-axis.

Please help!

 

[phinds]

You have not read the diagram carefully. The vertical axis is clearly marked "z", so one reasonably assumes that the y-axis is coming out of the paper, perpendicular to the cross section, thus your "problem" is solved.

 

[Adesh]

You have not read the diagram carefully. The vertical axis is clearly marked "z", so one reasonably assumes that the y-axis is coming out of the paper, perpendicular to the cross section, thus your "problem" is solved.

How our problem is solved? We knew that y-axis was perpendicular to the cross section. Please explain.

 

[phinds]

Ah, I see. I think the confusion is because the creation of the full boat, based on the cross section, is done by extending appropriate cross sections along the y axis. That is, parallel to the y axis. I misunderstood exactly what you were seeing as the problem where there isn't one.

 

[Ibix]

How our problem is solved? We knew that y-axis was perpendicular to the cross section. Please explain.

Your Wiki link, in its example section, says that the generatrices of a cone are straight lines in its surface through its apex, and for a cylinder are straight lines along its length (at least if you treat a cylinder as a limiting case of a cone). I think the book intends something similar for the boat - the generatrices are lines running along the length of the hull. By making them parallel to $y$ it is saying that the hull is remaining the same shape, neither widening nor narrowing, at least at this section of the ship.

 

[Adesh]

Thank you @phinds and @Ibix . The language of the book is quite confusing, because after this much explanation the book writes
Let $d\sigma$ be the surface element of the hull. According, to the simplified form of the hull $d\sigma= ds ~dy$ Where $ds$ is the line element of the cross section.

What does he mean by that? Does he mean that $d\sigma$ is a kind of rectangle whose lengths $ds$ lie on the cross-section and breadth is perpendicular to its length and lies in $y$ direction?

 

[Ibix]

The language of the book is quite confusing

The style of the book looks quite old, both the typeset and the language. I'd suggest something a bit more modern if you are having trouble with the language.

Let $d\sigma$ be the surface element of the hull. According, to the simplified form of the hull $d\sigma= ds ~dy$ Where $ds$ is the line element of the cross section.

What does he mean by that? Does he mean that $d\sigma$ is a kind of rectangle whose lengths $ds$ lie on the cross-section and breadth is perpendicular to its length and lies in $y$ direction?

You appear to have interpreted this particular passage correctly.