vish0096
- 3
- 0
I have a problem as shown in the figure
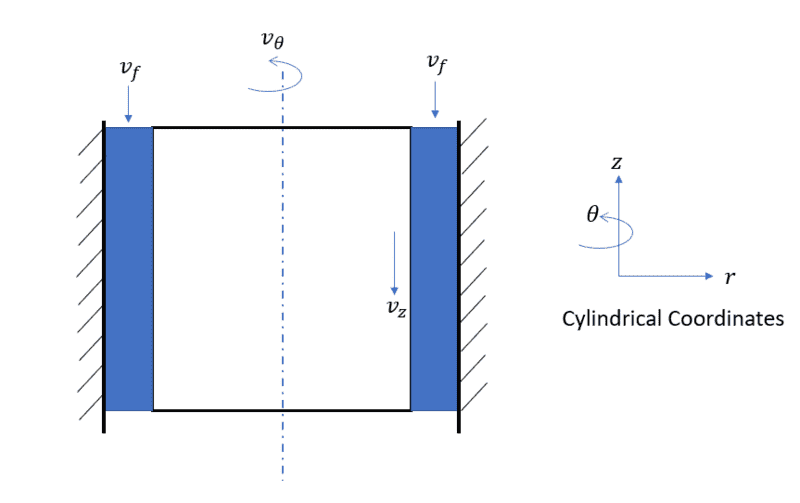
So assume there is a cylinder rotating inside a stationally wall. There is a viscous fluid in between the gap of cylinder wall and outer stationary wall, similar to bearing.
The fluid has some velocity in axial direction also
the outer wall of cylinder has velocity in the downward direction and
Moreover the cylinder is rotating about its axis so it will have a circumferential velocity as well.
Now I actually want to calculate the torque required to rotate this cylinder.
I have calculated the circumferetial and axial velocity
Then from that I have calculated the axial and circumferential component of torque, let say T_theta and T_z
Now how can I calculate the resultant torque?
Problem is these two torque act in two different planes, so I am not understanding how can I add them.
The shear forces causeing the torque are shown in the figure below
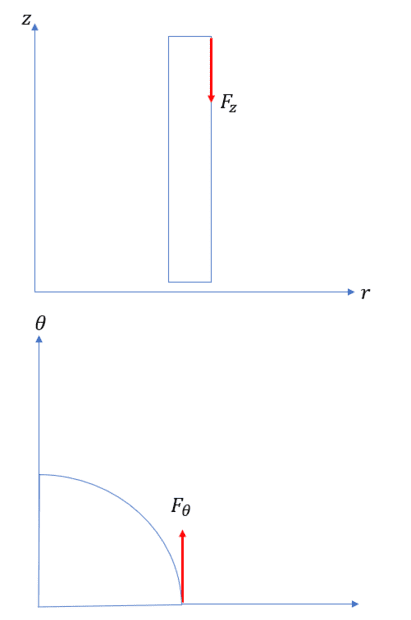
So assume there is a cylinder rotating inside a stationally wall. There is a viscous fluid in between the gap of cylinder wall and outer stationary wall, similar to bearing.
The fluid has some velocity in axial direction also
the outer wall of cylinder has velocity in the downward direction and
Moreover the cylinder is rotating about its axis so it will have a circumferential velocity as well.
Now I actually want to calculate the torque required to rotate this cylinder.
I have calculated the circumferetial and axial velocity
Then from that I have calculated the axial and circumferential component of torque, let say T_theta and T_z
Now how can I calculate the resultant torque?
Problem is these two torque act in two different planes, so I am not understanding how can I add them.
The shear forces causeing the torque are shown in the figure below