How can I calculate the derivative of this function?

[GaussianSurface]

Homework Statement

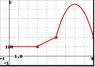
Let f(x) be the function whose graph is shown below (I'll upload the image)

Determine f'(a) for a = 1,2,4,7.

f'(1) =

f'(2) =

f'(4) =

f'(7) =

Use one decimal.

Homework Equations

f(x+h)-f(x)/h

The Attempt at a Solution

Hi everybody I was trying to do this function but I haven't been able to do it even though I'm supposing some things about how this problem can be compute, so I want to ask for help so some of you can guide me to the final result, hope some of you all can help me.

 

[MarkFL]

When consdering some function $f(x)$, what is a geometric interpretation of $f'(a)$?

 

[GaussianSurface]

When consdering some function $f(x)$, what is a geometric interpretation of $f'(a)$?

I guess it's not specified, actually I had the same problem I was wondering what's ƒ'(a) since it is not in the graph they gave me...

 

[MarkFL]

What I mean is, in your study of the derivative, what have you been taught that the derivative can represent geometrically, that is, in relation to the graph of the function?

 

[GaussianSurface]

What I mean is, in your study of the derivative, what have you been taught that the derivative can represent geometrically, that is, in relation to the graph of the function?

Well, it can represent the slope or the instantaneuos rate of change. that's how they've taught me, is that what you wanted to know?

 

[MarkFL]

Well, it can represent the slope or the instantaneuos rate of change. that's how they've taught me, is that what you wanted to know?

Yes, that's what I was after.

So, can you determine the instantaneous slope of the given function's graph at the given values of $a$?

 

[GaussianSurface]

Yes, that's what I was after.

So, can you determine the instantaneous slope of the given function's graph at the given values of $a$?

Let me see if I got you.

Since you asked about to determine the insatataneous slope I'd say that we can do it by the defnition of derivative ( the one that I posted above ) so far am I going in the good way?

 

[MarkFL]

Let me see if I got you.

Since you asked about to determine the insatataneous slope I'd say that we can do it by the defnition of derivative ( the one that I posted above ) so far am I going in the good way?

It's actually more simple than that...you can "eyeball" the slope of the function at the given points...

 

[GaussianSurface]

It's actually more simple than that...you can "eyeball" the slope of the function at the given points...

Mmmm... Shall I take the prime points at x and compare with f'(a) and so on...?

 

[NascentOxygen]

Place a dot on your curve above each of the x-values where you are asked to find a value for f’

This will highlight exactly which points on the plot are under discussion.

 

[MarkFL]

Mmmm... Shall I take the prime points at x and compare with f'(a) and so on...?

First, let's consider the function where $0<x<3$...we have a horizontal line...what is the slope of a horizontal line?

 

[GaussianSurface]

Place a dot on your curve above each of the x-values where you are asked to find a value for f’

This will highlight exactly which points on the plot are under discussion.

Ohh! I think got it when the prime values get x then a value f'(x) changes with it, doesn't it?

 

[NascentOxygen]

Ohh! I think got it when the prime values get x then a value f'(x) changes with it, doesn't it?

I can't decide whether you can see the answers or not. As MarkFL indicated, the values of f' in this exercise can be decided by mere inspection. Remember, f'(b) is the slope of the curve f around point b.