user366312
Gold Member
- 88
- 3
Problem Statement
I was watching a YouTube video regarding the calculation of expected return time of a Markov Chain.
I haven't understood the calculation of ##m_{12}##.
How could he write ##m_{12}=1+p_{11}m_{12}##? I have given a screenshot of the video.
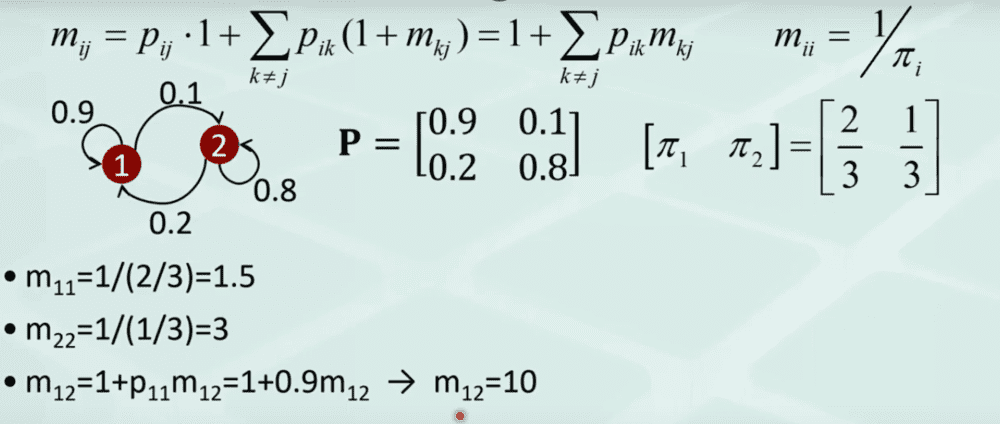
I was watching a YouTube video regarding the calculation of expected return time of a Markov Chain.
I haven't understood the calculation of ##m_{12}##.
How could he write ##m_{12}=1+p_{11}m_{12}##? I have given a screenshot of the video.
Last edited by a moderator: