RobertColman
- 5
- 0
Member advised to use the homework template for posts in the homework sections of PF.
I'm a bit stuck on this question (which is homework so hints are more welcome than outright answers). The question is:
A very long wire carrying a current I is moving with speed v towards a small circular wire loop of radius r. The long wire is in the plane of the loop and is too long to be entirely shown in the diagram.
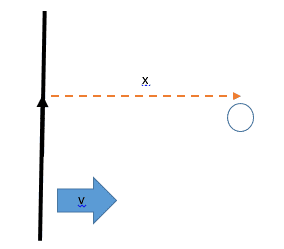
The strength of a magnetic field a distance x from a long wire is
$$|B|=\frac{μ_{0}I}{2πr}$$
What is the equation for the rate of change of the strength of the magnetic field at the centre of the loop?
As a hint we are given that $$V = \frac{dx}{dt}$$
Now, I can see that the equation for the strength of the field comes from amperes law, and is essentially the magnetic field along a loop around the wire, divided by the circumference of that loop.
So it makes sense to me that given everything else in the equation is constant, delta B should come straight from the change in the circumference of a circle as the radius shrinks. Now since
$$\frac{dC}{dt}=2\pi\frac{dr}{dt}$$
and since in this case $\displaystyle{\frac{dr}{dt}}$ is simply the velocity of the wire, it seems to me that the change in the field strength at the center of the loop should simply be
$$\frac{d|B|}{dt}=\frac{μ_{0}I}{2πV}$$
however I'm getting that this answer is wrong. Can anyone explain where I've made a mistake?
Thanks for your help.
A very long wire carrying a current I is moving with speed v towards a small circular wire loop of radius r. The long wire is in the plane of the loop and is too long to be entirely shown in the diagram.
The strength of a magnetic field a distance x from a long wire is
$$|B|=\frac{μ_{0}I}{2πr}$$
What is the equation for the rate of change of the strength of the magnetic field at the centre of the loop?
As a hint we are given that $$V = \frac{dx}{dt}$$
Now, I can see that the equation for the strength of the field comes from amperes law, and is essentially the magnetic field along a loop around the wire, divided by the circumference of that loop.
So it makes sense to me that given everything else in the equation is constant, delta B should come straight from the change in the circumference of a circle as the radius shrinks. Now since
$$\frac{dC}{dt}=2\pi\frac{dr}{dt}$$
and since in this case $\displaystyle{\frac{dr}{dt}}$ is simply the velocity of the wire, it seems to me that the change in the field strength at the center of the loop should simply be
$$\frac{d|B|}{dt}=\frac{μ_{0}I}{2πV}$$
however I'm getting that this answer is wrong. Can anyone explain where I've made a mistake?
Thanks for your help.