How can I find this formula for the magnetic flux density? (EMagn)

[Boltzman Oscillation]

Homework Statement

A semi-infinite linear conductor extends between z = 0 and z = inf. along the z- axis. If the current in the inductor flows along the positive z-direction find H(vector) at a point in the x-y plane at a distance r from the conductor.

Relevant Equations

H = I/(4*pi) Integral[( dl x R)/R^2]

I drew an illustration to make this easier:

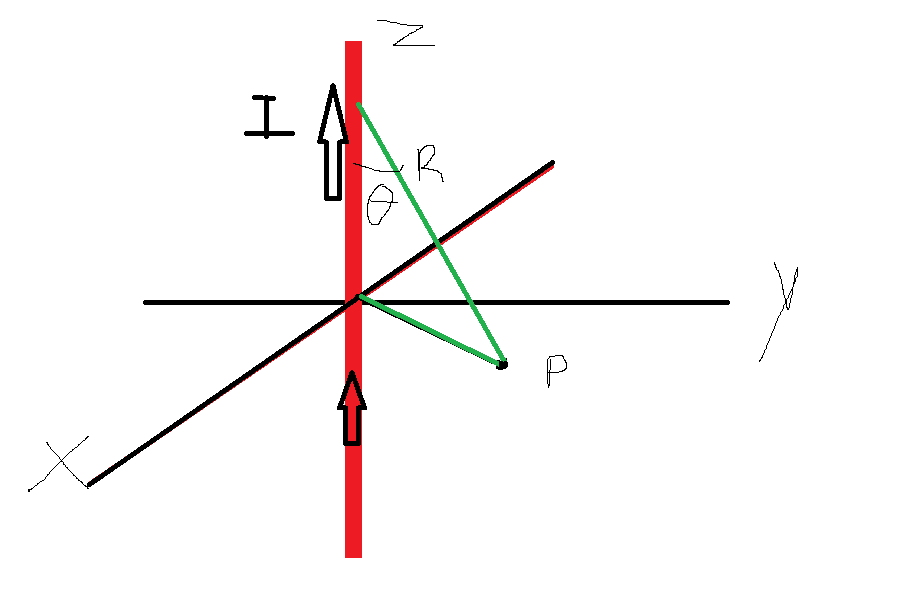
Point P is where I wish to find the magnetic flux density H.
Given the Biot-Savart formula:
$$d\textbf{H} = \frac{I}{4\pi}\frac{d\textbf{l}\times\textbf{R}}{R^2}$$
I can let
$$d\textbf{l} = \hat{z}dz$$
and
$$\hat{z}dz\times\textbf{R} = \hat{\phi}sin(\theta_{Rdl})dz$$
Have I done this correctly so far? If so, what should I let R^2 in the Biot-Savart equation be?

 

[Charles Link]

Looks ok. I'll give you a hint: What is $\frac{r}{R}$? One other hint is you would do well to also express $z$ in terms of $\theta$ and $r$, and write $dz$ as a $d \theta$ expression, and integrate over $\theta$.

 

[Boltzman Oscillation]

Looks ok. I'll give you a hint: What is $\frac{r}{R}$? One other hint is you would do well to also express $z$ in terms of $\theta$ and $r$, and write $dz$ as a $d \theta$ expression, and integrate over $\theta$.

Ah, I think I see what you mean.
$$R = rcsc(\theta)$$
$$z = rcsc^2(\theta)d\theta$$
$$dz = rcsc^2(\theta)d\theta$$
Thus Biot-Savart's law becomes:
Then doing all the integration from 0 to limiting angle will eventually lead me to:
$$H = \hat{\phi}\frac{I}{4\pi r}$$
Of course this is taking into account that this is a semi-infinite line.
thank you for that clarification.

 

[Charles Link]

Very good. The result for a whole wire running from $-\infty$ to $+\infty$ is twice this answer, and can readily be found from Ampere's law. You will likely see that soon also in your coursework.