SUMMARY
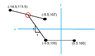
The discussion focuses on finding the intersection of two lines defined by the equations y = x + 105.5 and a line with a negative slope. The user initially miscalculated the slope, using +1 instead of the correct -1, leading to an incorrect intersection point of -1.87. The correct approach involves substituting the accurate slope into the equation to find an intersection point that is less than -5.5. The key takeaway is the importance of correctly identifying the slope's sign in linear equations.
PREREQUISITES
- Understanding of linear equations, specifically the slope-intercept form (y = mx + b).
- Knowledge of substitution methods for solving equations.
- Familiarity with graphing lines and identifying intersections.
- Basic algebra skills for manipulating equations.
NEXT STEPS
- Review the concept of slope in linear equations, focusing on negative slopes.
- Practice solving systems of equations using substitution and elimination methods.
- Learn how to graph linear equations accurately to visualize intersections.
- Explore the implications of slope changes on the intersection points of lines.
USEFUL FOR
Students studying algebra, particularly those working on linear equations and intersections, as well as educators looking for examples of common mistakes in slope calculations.