SwaGGeReR
- 6
- 0
I'm trying to plot something like x+y=2 in 3D. The image should look like this:
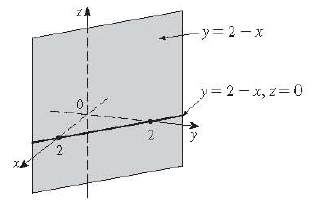
Been trying to do it in Mathematica using Plot3D, but the it treats the input as a function of z.
Another example: Plot3D[x=4,{x,0,10},{y,0,10},AxesLabel{x,y,z}] plots z=4, not x=4.
A similar thread, with no conclusive answer: https://www.physicsforums.com/showthread.php?t=101840
Been trying to do it in Mathematica using Plot3D, but the it treats the input as a function of z.
Another example: Plot3D[x=4,{x,0,10},{y,0,10},AxesLabel{x,y,z}] plots z=4, not x=4.
A similar thread, with no conclusive answer: https://www.physicsforums.com/showthread.php?t=101840
Last edited: