3d plot of interference from 2 wave sources with 2d grid surface

[BiGyElLoWhAt]

TL;DR Summary

Library suggestions or code snippets, either java or python (or wolfram query), to make a 2d mesh surface (with grid) that is the superposition of 2 decaying waves starting from 2 different points.

Desired output similar to image, but without the objects and with better wave interference:

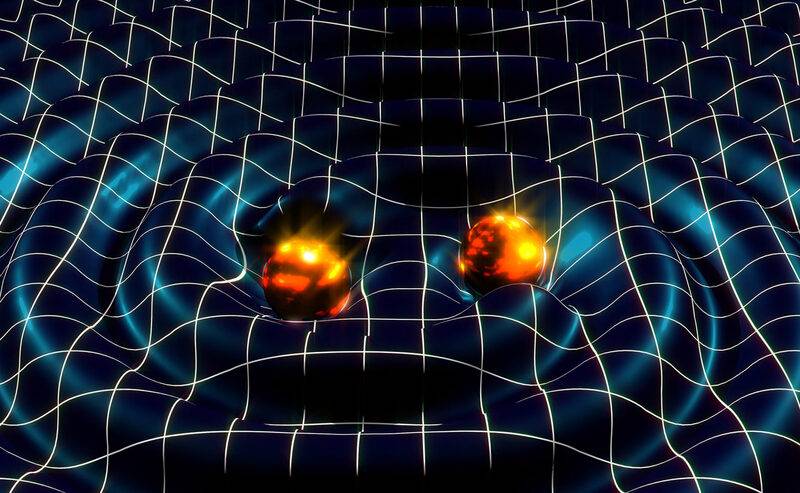
I tried plugging the following into wolfram (I specifically want the values to be adjustable):
plot z= H*e^(-m*sqrt((x-a)^2+(y-b)^2))*sin(k*(x-a)+k*(y-b) -w*t) + J*e^(-m*sqrt((x-c)^2+(y-d)^2))*sin(k*(x-c)+k*(y-d) -w*t), H=1, J=1, m=1, a=0, b=0, k=1, w=1, t=0, c=5, d=5

I've actually tried several variations on this including adding a 'for' before the variable list.
*Edit, removing "plot" gives some results, and it correctly interprets what I want, but doesn't give the plot*
I'm not sure if there is a specific way I need to plug this in to get an interactive plot, or if it just can't handle that many parameters. It keeps "interpreting as plot".

Any suggestions for library's/specific code snippets (or maybe there is already a program that basically does this?) that will help me make this surface grid are very much appreciated. I am pretty decent with java and python, but if maybe C/+/# are for some reason objectively better for this, I have experience with those as well.

I plan on adding sliders for the parameters listed at the end. Let me know if I left out anything crucial or if it's unclear what I'm after and I'll update the post as needed.

Thanks in advance.

 

[andrewkirk]

Have a look at this. Needed to hard-code some parameters cos Wolfram has a limit on number of characters.
Your formula had an error. The sine parts need to use the same distance formula (sqrt of sum of x and y distances) as the exp (attenuation) part.

plot e^(-1*sqrt(x^2+y^2))*sin(2*sqrt(x^2+y^2)-w*t)+e^(-1*sqrt((x-c)^2+(y-d)^2))*sin(2*sqrt((x-c)^2+(y-d)^2)-w*t) where w=1,t=0,c=5,d=5, for x from -5 to 10, y from -5 to 10

 

[BvU]

Hate to admit it, but excel () goes a long way...
(especially in combination with VB)

$\$