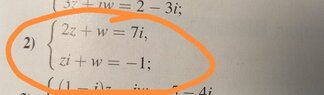How Can I Solve a System of Equations With Complex Numbers?

[Callmelucky]

Homework Statement

How can I solve a system of equations with complex numbers
2z+w=7i
zi+w=-1

Relevant Equations

z=a+bi

How can I solve a system of equations with complex numbers
2z+w=7i
zi+w=-1

I have tried substituting z with a+bi and I have tried substituting w=7i-2z but didn't get anything useful.

Edit: also, I've tried, multiplying lower eq. with -1 so that I can cancel w but I get stuck with 2z and zi and I can't figure out what I am supposed to do with that.

Edit2: also, I have tried replacing both z and w with a+bi but still nothing

Thank you

 

[PeroK]

How can I solve a system of equations with complex numbers
2z+w=7i
zi+w=-1

Are you sure you've typed that correctly?

 

[Callmelucky]

Are you sure you've typed that correctly?

yes, and the solution should be z=-1+3i, w=2+i

 

[FactChecker]

Edit: also, I've tried, multiplying lower eq. with -1 so that I can cancel w but I get stuck with 2z and zi and I can't figure out what I am supposed to do with that.

You can manipulate complex numbers very much like you are used to with real numbers.
So what you tried should give you 2z-zi = 7i-1. Then you can factor the left side to get z(2-i)=7i-1
CORRECTION: z(2-i)=7i+1 and divide both sides by 2-i. z=(-1+7i)/(2-i). CORRECTION: z=(1+7i)/(2-i)
(Corrections thanks to @pasmith)

Edit2: also, I have tried replacing both z and w with a+bi but still nothing

You can do that and work with all the reals and imaginary parts separately, but that is often the last resort.

 

[Mark44]

yes, and the solution should be z=-1+3i, w=2+i

I get these values.
You're making things harder than they need to be. Don't substitute a + ib for z. You can eliminate w by adding -1 times the second equation to the first. This gets you a simple equation involving only z. Then back-substitute to find w.

 

[Callmelucky]

So what you tried should give you 2z-zi = 7i-1. Then you can factor the left side to get z(2-i)=7i-1 and divide both sides by 2-i. z=(-1+7i)/(2-i).

I do get that, but that is not what is in solutions.

 

[pasmith]

You can manipulate complex numbers very much like you are used to with real numbers.
So what you tried should give you 2z-zi = 7i-1. Then you can factor the left side to get z(2-i)=7i-1 and divide both sides by 2-i. z=(-1+7i)/(2-i).

I do get that, but that is not what is in solutions.

Subtracting $iz + w = -1$ from $2z + w = 7i$ should give $$\begin{split} (2 - i)z + (1 - 1)w &= 7i - (-1) \\ (2 - i)z &= 1 + 7i.\end{split}$$

 

[FactChecker]

Okay, but that still isn't z=-1+3i

Yes, it is. You need to simplify it by multiplying both the numerator and denominator by 2+i

 

[Callmelucky]

I got it, that is why I deleted comment right after posting it lol :D.
Thanks everyone.

 

[Callmelucky]

But the problem is that I did not know how to divide complex numbers yesterday, I learned that like 10 minutes ago.

 

[Mark44]

But the problem is that I did not know how to divide complex numbers yesterday, I learned that like 10 minutes ago.

That's the key here. If you proceed as I advised back in post #5, you get $z = \frac{1 + 7i}{2 - i}$. If you don't know how to do division by complex numbers, you can't simplify the above to get $z = -1 + 3i$.

If you're working from a textbook, did it cover complex number division, but you didn't catch on?

 

[Callmelucky]

That's the key here. If you proceed as I advised back in post #5, you get $z = \frac{1 + 7i}{2 - i}$. If you don't know how to do division by complex numbers, you can't simplify the above to get $z = -1 + 3i$.

If you're working from a textbook, did it cover complex number division, but you didn't catch on?

But this is a task in the chapter before division, in the chapter for addition and multiplication of complex numbers.

 

[votingmachine]

When you get: z=(-1+7i)/(2-i).

multiply by (2+i)/(2+i)

 

[Mark44]

But this is a task in the chapter before division, in the chapter for addition and multiplication of complex numbers.

That seems odd. You didn't show the complete problem as it appears in the book -- were you supposed to solve for z and w, or was it something simpler, like saying that there is a solution vs. saying that there is no solution?

 

[Mark44]

Edit2: also, I have tried replacing both z and w with a+bi but still nothing

This works (although you can't replace both z and w with a + bi -- you need to replace w with a different complex number), but it entails knowing how to solve a system of four equations in four unknowns.

 

[SammyS]

But this is a task in the chapter before division, in the chapter for addition and multiplication of complex numbers.

Take the result @pasmith gave in Post#7, shown below.

Subtracting $iz + w = -1$ from $2z + w = 7i$ should give $$\begin{split} (2 - i)z + (1 - 1)w &= 7i - (-1) \\ (2 - i)z &= 1 + 7i.\end{split}$$

Now multiply both sides by the complex conjugate of $(2-i)$.

You will need to be able to divide both sides by $5$ to arrive at the answer..

 

[Callmelucky]

That seems odd. You didn't show the complete problem as it appears in the book -- were you supposed to solve for z and w, or was it something simpler, like saying that there is a solution vs. saying that there is no solution?

No, it says: solve systems of equations. And then 3 problems and that is it.

 

[Callmelucky]

This works (although you can't replace both z and w with a + bi -- you need to replace w with a different complex number), but it entails knowing how to solve a system of four equations in four unknowns.

I think this was expected to be done. Because I have already seen how it was supposed to be done just couldn't remember

 

[Mark44]

I think this was expected to be done. Because I have already seen how it was supposed to be done just couldn't remember

Yeah, if you write the system as an augmented matrix -- 4 rows and 5 columns, and do reduced row-echelon reduction, the solution comes out pretty easily.

 

[pbuk]

Take the result @pasmith gave in Post#7, shown below.

Now multiply both sides by the complex conjugate of $(2-i)$.

Yes that is one easy way without needing complex division - ISTR that multiplying by a complex conjugate was a common tool in solving exam questions at this stage.

It is also easy to solve by setting $z = a + ib, w = c + id$ and solving for the real and imaginary parts separately: you should get to e.g. $2a + b = 1, 2b - a = 7$ quickly and it is trivial from there.