MHB How Can I Visualize the Intersection of a Cone and a Sphere?

[Dethrone]

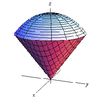
Find the volume of the solid that is enclosed by the cone $z=\sqrt{x^2+y^2}$ and the sphere $x^2+y^2+z^2=2$.

The integral is not difficult to set up using cylindrical coordinates, but I'm trying to get a better visualization of the volume I'm actually integrating. I can't seem to get Wolfram Alpha to graph both regions at the same time. Is there any way I can do that, or even better, have it to shade in that region?

(I have been able to graph it by hand, but it is a terrible sketch :( )

 

[Opalg]

I don't know what software is used for it, but a search for "spherical cone" leads to this:

View attachment 4457

(the source file is at Pauls Online Notes : Calculus III - Triple Integrals in Spherical Coordinates).