How Can One 2nd Order ODE Have Different Solutions?

[tade]

2nd Order ODE "Contradiction"?

To solve a 2nd order ODE, we can follow the steps as shown below. (Image 2 is a continuation from Image 1, apologies for the size difference.)

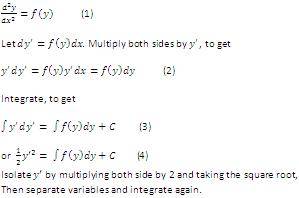
The method to obtain the solution is straightforward.

Let's say

\frac{d^2y}{dx^2}=ky

If k = -1, a possible solution is y = sin x. If k = 1, a possible solution is y = e^x.How do we obtain these two different solutions from one straightforward method?

 

[Mandelbroth]

Let's say

\frac{d^2y}{dx^2}=ky

If k = -1, a possible solution is y = sin x. If k = 1, a possible solution is y = e^x.


How do we obtain these two different solutions from one straightforward method?

I think Laplace transforms look good for this.

$$\frac{d^2y}{dx^2}=ky\implies\mathcal{L}\{\frac{d^2y}{dx^2}\}(s)=k \mathcal{L}\{y\}(s)\\ s^2\mathcal{L}\{y\}(s)-\left.\frac{dy}{dx}\right|_0-sy(0)=k\mathcal{L}\{y\}(s) \\ \mathcal{L}\{y\}(s)=\frac{\frac{dy}{dx}|_0+sy(0)}{s^2-k}\\y(x)=\mathcal{L}^{-1}\left\{\frac{\frac{dy}{dx}|_0+sy(0)}{s^2-k}\right\}(x).$$
With a bit of simplifying, this comes down to $y(x)=c_1e^{\sqrt{k}x}+c_2e^{-\sqrt{k}x}$.

Note that $\sin{x}=\frac{e^{ix}-e^{-ix}}{2i}$.

 

[tade]

With a bit of simplifying, this comes down to $y(x)=c_1e^{\sqrt{k}x}+c_2e^{-\sqrt{k}x}$.

Note that $\sin{x}=\frac{e^{ix}-e^{-ix}}{2i}$.

That's pretty neat.