struggling_student
- 9
- 1
I've been trying to derive a formula for diffraction pattern formed by casting a plane-wave through a generic 1D aperture onto a screen distanced ##L## from the aperture. The aperture is described by an opacity function ##f:\mathbb{R} \rightarrow [0,1]## so it can be a single slit, multiple slits, shaded glass with varying opacity. By the Huygens-Fresnel principle every point on that aperture is a spherical wave and we weigh them by infinitesimal ##du## so that it can be integrated.
Let ##u## be the position on the aperture relative to some chosen axis which also goes through the screen. Let the position on the screen relative to that axis be ##x##. The opacity function is a function of ##u##, i.e. ##f=f(u)##.
The wave that goes through point ##u## on reaching the screen has amplitude
$$A f(u) \cos\left(\frac{2\pi}{\lambda}\sqrt{(x-u)^2+L^2 }\right) du,$$
and the resulting diffraction will be
$$A \int_{\mathbb{R}} f(u) \cos\left(\frac{2\pi}{\lambda}\sqrt{(x-u)^2+L^2 }\right) du.$$
It's a function of ##x## and we would square it to get intensity. I'm not sure how to proceed or what I did wrong. This approach is the only approach I am interested in. I'm trying to obtaining something similar to Fourier transform. What's missing here?
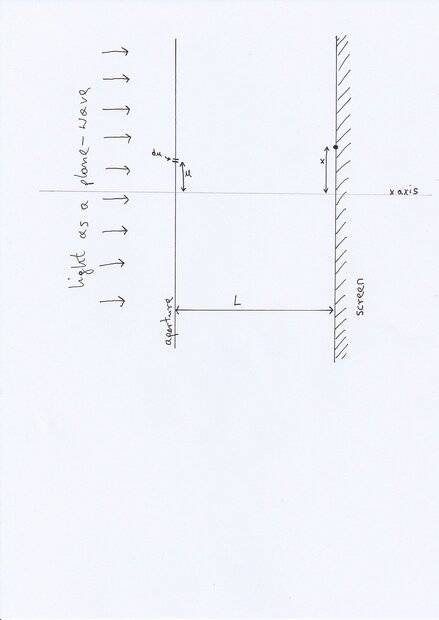
Let ##u## be the position on the aperture relative to some chosen axis which also goes through the screen. Let the position on the screen relative to that axis be ##x##. The opacity function is a function of ##u##, i.e. ##f=f(u)##.
The wave that goes through point ##u## on reaching the screen has amplitude
$$A f(u) \cos\left(\frac{2\pi}{\lambda}\sqrt{(x-u)^2+L^2 }\right) du,$$
and the resulting diffraction will be
$$A \int_{\mathbb{R}} f(u) \cos\left(\frac{2\pi}{\lambda}\sqrt{(x-u)^2+L^2 }\right) du.$$
It's a function of ##x## and we would square it to get intensity. I'm not sure how to proceed or what I did wrong. This approach is the only approach I am interested in. I'm trying to obtaining something similar to Fourier transform. What's missing here?