- #1
LmdL
- 73
- 1
Hello,
I'm trying to understand how can I compute a phase graph from diffraction. I will follow here Fourier transform formalism of finding the light distribution on screen after diffraction.
I'm considering a 1D problem. Suppose I have a single slit of width a. This slit can be mathematically written as:
[tex]y=Arect\left ( \frac{x}{a} \right )\bigotimes \delta \left ( 0 \right )[/tex]
i.e it is some amplitude A, multiplied by a rectangular function of width "a" with a convolution with delta function, since it's at origin.
Diffraction pattern is given by a Fourier transform:
[tex]Y=Aasinc\left ( \pi ka \right )[/tex]
So, the amplitude of the resulting diffraction pattern is given above (roughly ~sinc function). Spatial friquency k is:
[tex]k=\frac{x}{\lambda D}[/tex]
Where x is a position on the screen, D is the distance from the slit to the screen and lambda is a wavelength.
The intensity distribution on the screen is then:
[tex]I=\left |Y \right |^2=A^2a^2sinc^2\left ( \pi ka \right )[/tex]
Till now everything is fine. But in order to get the slit image, i.e. performing an inverse Fourier transform, I need both amplitude and phase. Amplitude I have calculated above (~sinc), but what is a phase as a function of x (position on the screen)? Is it zero everywhere? I know that phase in this case will be zero at point where amplitude is positive and pi at points where amplitude is negave:
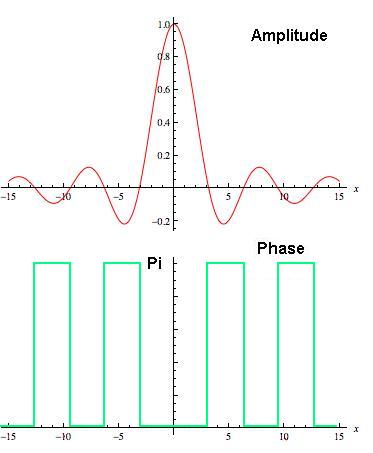
But how do I see the phase vs x from the diffraction pattern distribution?
Thanks!
I'm trying to understand how can I compute a phase graph from diffraction. I will follow here Fourier transform formalism of finding the light distribution on screen after diffraction.
I'm considering a 1D problem. Suppose I have a single slit of width a. This slit can be mathematically written as:
[tex]y=Arect\left ( \frac{x}{a} \right )\bigotimes \delta \left ( 0 \right )[/tex]
i.e it is some amplitude A, multiplied by a rectangular function of width "a" with a convolution with delta function, since it's at origin.
Diffraction pattern is given by a Fourier transform:
[tex]Y=Aasinc\left ( \pi ka \right )[/tex]
So, the amplitude of the resulting diffraction pattern is given above (roughly ~sinc function). Spatial friquency k is:
[tex]k=\frac{x}{\lambda D}[/tex]
Where x is a position on the screen, D is the distance from the slit to the screen and lambda is a wavelength.
The intensity distribution on the screen is then:
[tex]I=\left |Y \right |^2=A^2a^2sinc^2\left ( \pi ka \right )[/tex]
Till now everything is fine. But in order to get the slit image, i.e. performing an inverse Fourier transform, I need both amplitude and phase. Amplitude I have calculated above (~sinc), but what is a phase as a function of x (position on the screen)? Is it zero everywhere? I know that phase in this case will be zero at point where amplitude is positive and pi at points where amplitude is negave:

But how do I see the phase vs x from the diffraction pattern distribution?
Thanks!