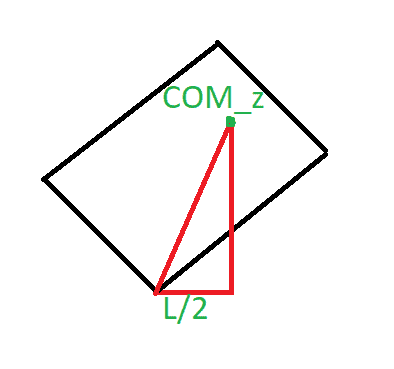
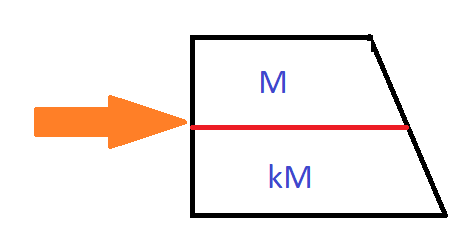
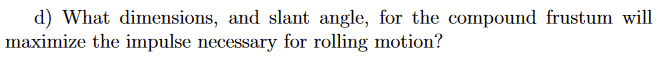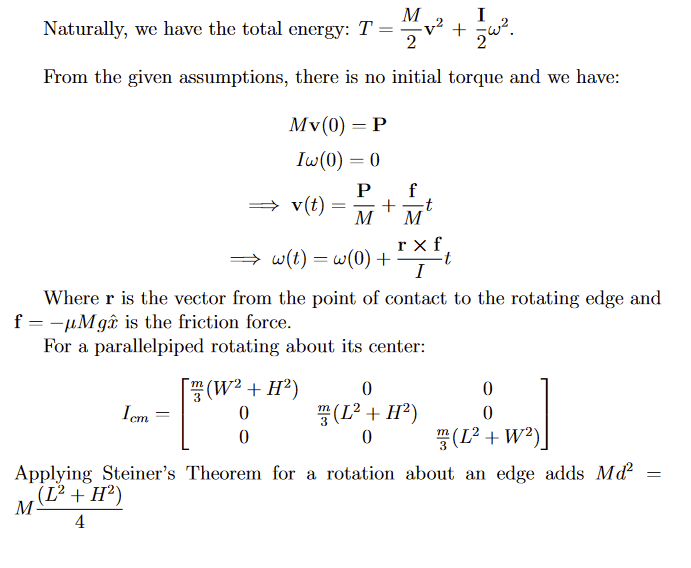SUMMARY
The discussion centers on the innovative concept of integrating rectangular prisms into billiards, enhancing the traditional gameplay. Participants express enthusiasm for the potential challenges posed by calculating angles and trajectories when balls interact with the prisms. Suggestions include using the prisms as pockets or obstacles, which would necessitate strategic thinking and precise aiming. The idea of varying sizes and shapes of prisms is also highlighted as a way to increase complexity and excitement in the game.
PREREQUISITES
- Understanding of billiards gameplay mechanics
- Basic knowledge of geometry and angles
- Familiarity with game design principles
- Experience in strategic thinking and problem-solving
NEXT STEPS
- Research the physics of angles and trajectories in billiards
- Explore game design techniques for incorporating obstacles
- Investigate variations of billiards games and their mechanics
- Experiment with creating prototypes of billiards tables featuring prisms
USEFUL FOR
This discussion is beneficial for game designers, billiards enthusiasts, and anyone interested in innovative gameplay mechanics and strategic game development.