astrozilla
- 28
- 0
Homework Statement
A gaseous system has an internal energy U which can be expressed
U=2.5pV +constant
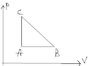
The system is initially in A. (attatchement)
The system goes from A to B ,B to C, C to A.
How can we find the work done on the Gas and the heat input to the gas in each for the three processes.
The total work done for the cycle is zero?
Homework Equations
W(Intergral from A to B)[pdV] is a possible candidate equation. Can also the general equationU=2.5pV+constant be related with the equation U=W+Q ?!
The Attempt at a Solution
I suspect that the total work done i.e Wabca must be zero. Also to find the work from B to C ,maybe the area under the line B C can be used.My current physics experience does not allow me to think anything else that can help.
Attachments
Last edited: