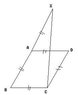
SUMMARY
The discussion centers on proving that angle XCB is 90 degrees in a parallelogram ABCD, where BA is extended to point X such that BA = AX. Participants clarify that this proposition is generally false, as demonstrated by counterexamples, including a square where angle XCB is not a right angle. The angle XCB can only be 90 degrees under specific conditions, such as when ABCD is a rhombus with internal angles of 60 and 120 degrees. The conclusion emphasizes that without restrictions on the dimensions or angles of the parallelogram, angle XCB will not universally equal 90 degrees.
PREREQUISITES
- Understanding of parallelogram properties
- Knowledge of trigonometric functions, specifically tangent
- Familiarity with geometric proofs and counterexamples
- Ability to interpret and create geometric diagrams
NEXT STEPS
- Study the properties of rhombuses and their angles
- Learn about the conditions under which angles in parallelograms are right angles
- Explore geometric proofs involving trigonometric identities
- Investigate the relationship between side lengths and angles in various types of quadrilaterals
USEFUL FOR
Mathematicians, geometry students, educators, and anyone interested in understanding the properties of parallelograms and geometric proofs.