- #1
erocored
- 30
- 7
I know he had this ratio:
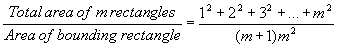
But how did he get this:
?
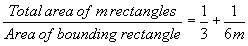But how did he get this:
How did Cavalieri get his formula for the area underneath a parabola?
Click For Summary
SUMMARY
Cavalieri derived his formula for the area underneath a parabola using the sum of squares formula: $$\sum_{k=1}^m k^2 = \frac{m(m + 1)(2m + 1)}{6}$$. By substituting the sum of squares into his initial equation, he was able to achieve the desired result. This method highlights the significance of mathematical ratios and summation techniques in deriving geometric properties.
PREREQUISITES- Understanding of calculus concepts, specifically integration.
- Familiarity with the sum of squares formula.
- Basic knowledge of geometric properties of parabolas.
- Experience with mathematical proofs and derivations.
- Study the derivation of the sum of squares formula in detail.
- Explore Cavalieri's principle and its applications in geometry.
- Learn about integration techniques for calculating areas under curves.
- Investigate other historical methods of area calculation in mathematics.
Mathematicians, educators, students studying calculus, and anyone interested in the historical development of geometric formulas.
- #2
erocored
- 30
- 7
- #3
Mark44
Mentor
- 38,079
- 10,609
The result uses a formula for the sum of squares.erocored said:
$$\sum_{k=1}^m k^2 = \frac{m(m + 1)(2m + 1)}6$$
Replace ##1^2 + 2^2 + \dots + m^2## in your first equation by the above, and you will get the result shown in the second equation.
Similar threads
- · Replies 2 ·
- · Replies 22 ·
- · Replies 3 ·
High School
Question about volume of a sphere
- · Replies 16 ·
- · Replies 3 ·
Undergrad
The surface area of an oblate ellipsoid
- · Replies 8 ·
- · Replies 49 ·
- · Replies 3 ·
Undergrad
Jacobian transformation for finding area
- · Replies 1 ·
- · Replies 2 ·