How do I add vectors using geometric and component-wise methods?

[Jtechguy21]

Homework Statement

Hello, this is my first time taking physics in college, and I have read the section twice and I this is what I understand. If someone could point me in the right direction, that would be great.

For example:
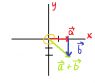
How do I find the angle for example from Vector a + Vector b.
Would I use the tail to head method and that would give me a reference angle of 90 degrees, and rank accordingly? Or am i missing something here

Homework Equations

hint1)
The vector resulting from the combination a⃗ +b⃗ is the only vector that lies outside of the first quadrant. The first quadrant is the portion of the xy coordinate axes that lies between the positive x-axis and the positive y axis.

hint2)
You may add the vectors either geometrically or by determining the components of the vectors and adding component-wise. Once you have done the necessary vector additions, you can measure the angles from the positive x-axis counterclockwise to the resultant vectors.

The Attempt at a Solution

 

[jackarms]

Yes, you can use that method to add the vectors together and then find the angle of the resultant vector. You could also find the resultant with components, but since you're given all the vectors, it's probably easiest to just draw the additions off to the side.

So you want to draw the vectors on the head of the previous vector, then draw the resultant vector from the tail of the first vector to the head of the last vector, then find the angle for the resultant vector. So for example, $\vec{a} + \vec{b}$ gives a vector that points into the fourth quadrant, and the angle with respect to the x-axis will actually be -45 degrees, or, equivalently, 315 degrees.

 

[Jtechguy21]

Yes, you can use that method to add the vectors together and then find the angle of the resultant vector. You could also find the resultant with components, but since you're given all the vectors, it's probably easiest to just draw the additions off to the side.

So you want to draw the vectors on the head of the previous vector, then draw the resultant vector from the tail of the first vector to the head of the last vector, then find the angle for the resultant vector. So for example, $\vec{a} + \vec{b}$ gives a vector that points into the fourth quadrant, and the angle with respect to the x-axis will actually be -45 degrees, or, equivalently, 315 degrees.

Could you pleas explain how vector A+B = -45degrees?
I do see that it points on the fourth quadrant.

Whats confusing me the most is what does it exactly mean to be measured counterclockwise from the positive x axis.

 

[jackarms]

It means the angle that gets traced if you start at the x-axis and then go counterclockwise to the vector.

Imagine a rotating bar that is hinged at the origin and only rotates counterclockwise, and starts out overlaping the positive x axis. How much of a full rotation would it take to get the bar to overlap the resultant vector, in this case $\vec{a} + \vec{b}$?

If you've ever worked with the unit circle, this is the same principle. The angles of the unit circle are also measured from the positive x axis, so matching those up with where a vector points is another way of finding the angle.

And finally, if you must use it, the definition of the angle $\Theta$ a vector $u$ makes w/ respect to the x-axis is as follows:
$$\Theta = arctan(\frac{u.y}{u.x})$$

 

[Jtechguy21]

It means the angle that gets traced if you start at the x-axis and then go counterclockwise to the vector.

Imagine a rotating bar that is hinged at the origin and only rotates counterclockwise, and starts out overlaping the positive x axis. How much of a full rotation would it take to get the bar to overlap the resultant vector, in this case $\vec{a} + \vec{b}$?

If you've ever worked with the unit circle, this is the same principle. The angles of the unit circle are also measured from the positive x axis, so matching those up with where a vector points is another way of finding the angle.

And finally, if you must use it, the definition of the angle $\Theta$ a vector $u$ makes w/ respect to the x-axis is as follows:
$$\Theta = arctan(\frac{u.y}{u.x})$$

Thank you so much for trying to help me.
Can you please explain to me one more time why exactly does the vector a+ vector b= 315 degrees?
I just don't see it. When you add both the vectors it forms a 90 degree angle pointing down in the fourth quadrant, is that correct? I'm still having troubles understanding.

 

[jackarms]

You might be confusing the angle a resultant makes with the angle the individual vectors make. In this case, $\vec{a}$ does make a 90 degree angle with $\vec{b}$, but this is separate from the angle a resultant makes. I attached a picture below (really should have made this earlier! It's so hard to talk about vectors without a picture, as you can probably tell, haha)

Here you can see that $\vec{a}$ and $\vec{b}$ make a right angle, but the angle you're looking for is that of the resultant -- the green vector. That's the orange angle I marked in the diagram. Hopefully that's a better way to describe what measuring counterclockwise from the x-axis -- you can draw an arc from the x-axis and go counterclockwise until you hit the vector whose angle you want to measure, and then you see what the angle of the arc is.

 

[Jtechguy21]

You might be confusing the angle a resultant makes with the angle the individual vectors make. In this case, $\vec{a}$ does make a 90 degree angle with $\vec{b}$, but this is separate from the angle a resultant makes. I attached a picture below (really should have made this earlier! It's so hard to talk about vectors without a picture, as you can probably tell, haha)

Here you can see that $\vec{a}$ and $\vec{b}$ make a right angle, but the angle you're looking for is that of the resultant -- the green vector. That's the orange angle I marked in the diagram. Hopefully that's a better way to describe what measuring counterclockwise from the x-axis -- you can draw an arc from the x-axis and go counterclockwise until you hit the vector whose angle you want to measure, and then you see what the angle of the arc is.

Thank you so much this all makes perfect sense to me! I appreciate the time you've taken to help me understand this. )

 

[jackarms]

No problem! Glad you got it all sorted out. :)