arhzz
- 284
- 58
- Homework Statement
- Draw the bodediagram
- Relevant Equations
- -
Hello! I have this filter here
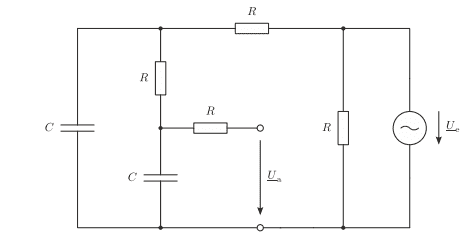
a)
Calculate the transfer function T(Ω) = Ua/Ue using voltage dividers.For this, use the normalized angular frequency Ω = ωRC and bring the result into the form ##T(Ω) = \frac{A+jB}{C+jD} ## . The result must not contain any double fractions.
I was able to that I have redrawn the circuit and used a double voltage divider to get this result
$$ \frac {1}{ 1 - Ω^2 + j3Ω} $$ and I think it should be correct
b)In general, calculate the absolute value |T(Ω)| and the phase arg(T(Ω)) of the transfer function. It must not be conjugated complex.
So for the absolute value I did this $$ sqrt{\frac{1}{(1-Ω^2)^2+(3Ω)^2}}$$ since its only general. And for the phase I think it should be
##arg(T(Ω)) = arctan(\frac{Im}{Re}) - arctan(\frac{Im}{Re})## where the first arctan is the one from the nummerator and the second one from the denominator. Since the first one is 0 what remains is ; ## - arctan(\frac{3Ω}{1-Ω^2}) ##
c) What kind and order of filter does the above circuit represent?
It is a low pass , 2nd order
d) Calculate the 3 dB limit frequency Ωg with |T max| = |T(Ω → 0)|.
I was also able to this since $$|T(Ω)| = \frac{Tmax){\sqrt{2}} $$ and after solving it I get that Ωg = 0,37
Now up to this point I had no real issues and all of my solutions match the one from the book. But here is where I am kind of stumped
e) sketch the Bode diagram (magnitude and phase) as a function of the normalized angular frequencyΩ. Calculate the magnitude and phase of the transfer function for ̈Ω=[0.1, 0.4, 0.6, 0.8, 1, 2, 4,90]and interpolate the values in between.Continue to draw the asymptote in the diagramm.
Now I am not really sure how to do this. I mean I could just plug in the values for omega into the equations but I have no cutoff frequency. I know what a bode diagramm of a low pass filter looks like and how to calculate the cutoff frequency of one but I have no values for C and R. Can I draw it without the cutoff frequency? Also I am not sure how to interpolate the values in between (we have not done it before in class). For the asymptote I know what it is (at least what I've learned in mathematics) it is susposed to be the line that the graph approaches but never touches. I am guessing this will be apperent when I draw the graph.
So how should I approach this? Should I just plug in the values draw and see what kind of graph comes out? Disregarding the cutoff frequency?
a)
Calculate the transfer function T(Ω) = Ua/Ue using voltage dividers.For this, use the normalized angular frequency Ω = ωRC and bring the result into the form ##T(Ω) = \frac{A+jB}{C+jD} ## . The result must not contain any double fractions.
I was able to that I have redrawn the circuit and used a double voltage divider to get this result
$$ \frac {1}{ 1 - Ω^2 + j3Ω} $$ and I think it should be correct
b)In general, calculate the absolute value |T(Ω)| and the phase arg(T(Ω)) of the transfer function. It must not be conjugated complex.
So for the absolute value I did this $$ sqrt{\frac{1}{(1-Ω^2)^2+(3Ω)^2}}$$ since its only general. And for the phase I think it should be
##arg(T(Ω)) = arctan(\frac{Im}{Re}) - arctan(\frac{Im}{Re})## where the first arctan is the one from the nummerator and the second one from the denominator. Since the first one is 0 what remains is ; ## - arctan(\frac{3Ω}{1-Ω^2}) ##
c) What kind and order of filter does the above circuit represent?
It is a low pass , 2nd order
d) Calculate the 3 dB limit frequency Ωg with |T max| = |T(Ω → 0)|.
I was also able to this since $$|T(Ω)| = \frac{Tmax){\sqrt{2}} $$ and after solving it I get that Ωg = 0,37
Now up to this point I had no real issues and all of my solutions match the one from the book. But here is where I am kind of stumped
e) sketch the Bode diagram (magnitude and phase) as a function of the normalized angular frequencyΩ. Calculate the magnitude and phase of the transfer function for ̈Ω=[0.1, 0.4, 0.6, 0.8, 1, 2, 4,90]and interpolate the values in between.Continue to draw the asymptote in the diagramm.
Now I am not really sure how to do this. I mean I could just plug in the values for omega into the equations but I have no cutoff frequency. I know what a bode diagramm of a low pass filter looks like and how to calculate the cutoff frequency of one but I have no values for C and R. Can I draw it without the cutoff frequency? Also I am not sure how to interpolate the values in between (we have not done it before in class). For the asymptote I know what it is (at least what I've learned in mathematics) it is susposed to be the line that the graph approaches but never touches. I am guessing this will be apperent when I draw the graph.
So how should I approach this? Should I just plug in the values draw and see what kind of graph comes out? Disregarding the cutoff frequency?