hamza2095
- 28
- 1
I designed this game for my Data class but I'm having a lot of trouble calculating the expected profit per play of this game. We have taken up examples involving lottery tickets in which you have to calculate the profit and winning per ticket bought but I can't seem to apply the same concepts to my game due to the various stages and rules.
This is how the games goes
You pay $20 to start and there are three rounds
Round 1: There is a 1/2 chance you win and move on, and a 1/2 chance you lose
Round 2: There is a 2/6 chance you move on to the next round, and 1/6 chance you win $10 AND move on. (3/6 chance you lose and get nothing)
Round 3: There is 1/12 chance you win $100, and if you lose you get nothing
Here is my attempt at it
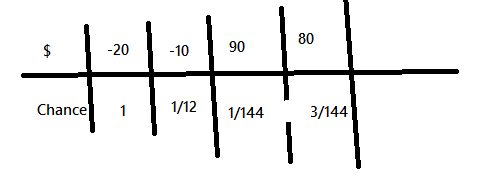
After multiplying every correlating x and y value i get E(X) = -18.5, meaning the profit the ones running the game make is $18.5
Help is greatly appreciated!
This is how the games goes
You pay $20 to start and there are three rounds
Round 1: There is a 1/2 chance you win and move on, and a 1/2 chance you lose
Round 2: There is a 2/6 chance you move on to the next round, and 1/6 chance you win $10 AND move on. (3/6 chance you lose and get nothing)
Round 3: There is 1/12 chance you win $100, and if you lose you get nothing
Here is my attempt at it
After multiplying every correlating x and y value i get E(X) = -18.5, meaning the profit the ones running the game make is $18.5
Help is greatly appreciated!