How do I Graph the Sine Function for y=2-sin(2πx/3)?

[FritoTaco]

Homework Statement

Problem: y=2-sin\dfrac{2\pi x}{3}

Homework Equations

Standard Equation: y = A sin(B(x - C)) + D

• A: amplitude is A
• B: period is \dfrac{2\pi}{|b|}
• C: phase shift is \dfrac{C}{B}
• D: vertical shift is D

Count Formula: \dfrac{1}{4}\cdot period (What you use to choose your x-values)

The Attempt at a Solution

First, rearrange the equation: y=-sin\dfrac{2\pi x}{3}+2

Amplitude: 1 (a-value)
Period: \dfrac{2\pi}{2\pi/3}=\dfrac{2\pi}{1}\cdot\dfrac{3}{2\pi}=\dfrac{6\pi}{2}=3\pi
Phase Shift: 0 (no c-value)
Vertical Shift: 2 (d-value)

Table (I don't know how to make):
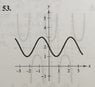
See my attachment for the table of values.

How did I pick my x-values to calculate my y-values?
I used count formula: \dfrac{1}{4}\cdot \dfrac{3\pi}{1}=\dfrac{3\pi}{4}
So, I start from the phase shift and continue adding \dfrac{3\pi}{4} : 0+\dfrac{3\pi}{4}=\dfrac{3\pi}{4}
\dfrac{3\pi}{4}+\dfrac{3\pi}{4}=\dfrac{6\pi}{4}=\dfrac{3\pi}{2}
\dfrac{3\pi}{2}+\dfrac{3\pi}{4}=\dfrac{6\pi}{4}+\dfrac{3\pi}{4}=\dfrac{9\pi}{4}
\dfrac{9\pi}{4}+\dfrac{3\pi}{4}=\dfrac{12\pi}{4}=3\pi

I don't want to graph it yet because my table of values doesn't seem correct, in my book the answer is in my second attachment. They don't even use pi for their x-values :(

 

[lurflurf]

Your period is wrong 3 not 3 pi
All the functions in that family do the same thing
High middle low middle high and so on
We just need one value which state it is then the differences to generate a table
You can add more points too if desired
Vertical change 1 amplitude
Horizontal change .75 period/4
Make a table with horizontal coordinates multiples of 0.75
Multiples of 1.5 have value 2
-3 2
-2.25 1
-1.5 2
-0.75 3
0 2
.75 1
1.5 2
2.25 3
3 2

 

[FritoTaco]

Multiples of 1.5 have value 2
-3 2
-2.25 1
-1.5 2
-0.75 3
0 2
.75 1
1.5 2
2.25 3
3 2

Wait, so why are we multiplying are each time by \dfrac{3}{4}? Actually I'm not sure what you are doing. My teacher told me to keep adding it to find new x-values? Where you got 1.5, I got \dfrac{6}{4}=\dfrac{3}{2}

 

[LCKurtz]

Where you got 1.5, I got \dfrac{6}{4}=\dfrac{3}{2}

$$\frac 3 2 = 1.5$$

 

[FritoTaco]

But how do the x-values come about? I'm confused.

 

[lurflurf]

start at zero and add or subtract 0.75=3/5
add
0+0.75=0.75
.75+0.75=1.5
1.5+0.75=2.25
2.25+0.75=3
subtract
0-0.75=-0.75
.75-0.75=-1.5
1.5-0.75=-2.25
2.25-0.75=-3

we choose 0.75 because it is p/4=3/4=.075

 

[FritoTaco]

Oh I see, but how did you get the y-values. Like at 0, you have 2 for y value. In my picture I have, I got 1 for my y-value.

 

[lurflurf]

We plot sin(x) for reference using values

$$

\left| \begin{array}{c|c}
x & \sin(x) \\
\hline
-\pi & 0 \\
-\pi/2 & -1\\
0 & 0 \\
\pi/2 & 1\\
\pi & 0\\
\end{array} \right|

$$
We can use more points if we like either to show more periods or more details.

The general case is just shifts and flips and dilation of sin(x)
$$\left| \begin{array}{c|c}
x &A \sin(B(x-C))+D \\
\hline
C-\pi/B & D \\
C-\pi/(2B) & D-A\\
C & D \\
C+\pi/(2B) & D+A\\
C+\pi/B & D\\
\end{array} \right|

$$
including your case
$$\left| \begin{array}{c|c}
x &2- \sin(2\pi x/3) \\
\hline
0-1.5 & 2 \\
0-1.5/2 & 2+1\\
0 & 2 \\
0+1.5/2 & 2-1\\
0+1.5 & 2\\
\end{array} \right|

$$

 

[FritoTaco]

including your case
$$\left| \begin{array}{c|c}
x &2- \sin(2\pi x/3) \\
\hline
0-1.5 & 2 \\
0-1.5/2 & 2+1\\
0 & 2 \\
0+1.5/2 & 2-1\\
0+1.5 & 2\\
\end{array} \right|

$$

Oh, I should be including the +2 from my equation. Thanks!