How Do Kirchhoff's Laws Apply to a Capacitor in a Circuit?

[Saraphim]

Homework Statement

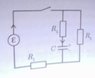
The problem considers the diagram in the photo that I have attached. Apologies for the poor quality, but sketching it on my computer would have been even worse!

a) Write down Kirchhoff's laws for the circuit and show that when the switch is closed, the charge on the capacitor Q behaves according to:
\frac{R_2}{R_1+R_2}\epsilon = \frac{Q}{C}+\left(R_3+\frac{R_1 R_2}{R_1+R_2}\right)\frac{dQ}{dt}

Homework Equations

The current through the branch with the capacitor, I_3, can be described by dQ/dt.

The Attempt at a Solution

First, Kirchhoff's laws.

The node law says that I_1=I_2+I_3.

Then the mesh laws, I get three meshes:

\epsilon=I_1 R_1 + I_2 R_2
\epsilon=I_1 R_1 + I_3 R_3+ \frac{Q}{C}
0=I_3 R_3 + \frac{Q}{C} - I_2 R_2

I'm fairly sure those are correct, however, I can't figure out how to combine these to show the differential equation given in the problem statement. I think I must leave out one of the relations obtained from the mesh law, but I have no idea where to start, or how to proceed in any sort of methodical way. Any pointers would be greatly appreciated, I'm sure I can work it out if I just get a nudge in the right direction!

 

[ehild]

\epsilon=I_1 R_1 + I_2 R_2
\epsilon=I_1 R_1 + I_3 R_3+ \frac{Q}{C}
0=I_3 R_3 + \frac{Q}{C} - I_2 R_2

The circuit contains two independent meshes. Omit the third mesh equation, it is not independent from the previous ones. Use the equation I1=I2+I3 and the first mesh equation to get I1 in terms of I3. Substitute for I1 in the second mesh equation. Use dQ/dt for I3.

ehild

 

[Saraphim]

So the first independent mesh is the one containing R1 and R3 and the other containing R3 and R2?

 

[Saraphim]

Wait, no, that's wrong. I'll think on it some more.

 

[Saraphim]

I can't seem to find out which two meshes are independent.

 

[ehild]

Any two ones. ehild