How do the magnetic fields produce emfs?

[ghostfolk]

I should add context to this question that what I know so far of the emf is that it is defined as $\mathscr E=\oint f \cdot d\ell$ where $f$ is the sum of the forces on the charges. In the textbook I'm reading it gives an example of where a person pulls a rectangular wire with a velocity $\vec{v}$ and the left side of that wire is in a uniform magnetic field.

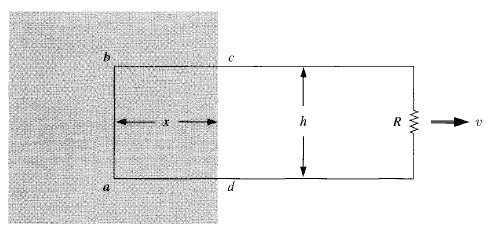
After some calculations, the author states that calculating the emf from the current induced in line $ab$ at a particular instant is equivalent to the work done by the person pulling the wire even though the force of the magnetic field, $\vec{v}\times \vec{B}$, has no effect on the work done by the person and the force exerted by the person, $f_{pull}$ has no effect on the emf. How is that we can interpret the emf as $\begin{equation} \mathscr E=\int f_{pull} \cdot d\ell=\oint f_{mag} \cdot d\ell\end{equation}$, yet the force produced by a magnetic field does no work?

 

[Simon Bridge]

It is not clear where the problem lies: your post describes how moving a wire in a magnetic field gets you and emf.
The magnetic force does no work because it acts perpendicular to the displacement of the charge.
The work needed to generate the energy in the circuit is provided by whatever is pulling the wire... you can see this if you try dropping a conductor past a magnet.

 

[ghostfolk]

It is not clear where the problem lies: your post describes how moving a wire in a magnetic field gets you and emf.
The magnetic force does no work because it acts perpendicular to the displacement of the charge.
The work needed to generate the energy in the circuit is provided by whatever is pulling the wire... you can see this if you try dropping a conductor past a magnet.

Then why can say the the magnetic field produces an emf if the one pulling the wire is providing the energy?

 

[Simon Bridge]

You get an emf by pulling a wire through a magnetic field.
Work out the forces on a charge in the wire.

 

[ghostfolk]

You get an emf by pulling a wire through a magnetic field.
Work out the forces on a charge in the wire.

My issue is that I have been thinking of the force produced by the magnetic field as something similar to the normal force in mechanics. Both only affect the way the object's path, but do no work. So it's confusing to me how the magnetic force can push charges around a wire.

 

[vanhees71]

One more hint: The correct integral form of Faraday's Law is
$$\mathcal{E}=\int_{\partial F} \mathrm{d} \vec{r} \cdot \left (\vec{E}+\frac{\vec{v}}{c} \times \vec{B} \right)=-\frac{\mathrm{d}}{\mathrm{d} t} \int_{F} \mathrm{d}^2 \vec{f} \cdot \vec{B}.$$
Here, $\vec{v}=\vec{v}(t,\vec{x})$ is the velocity of the boundary $\partial F$ of the surface $F$.

Further you know Ohm's Law, $\mathcal{E}=R I$ if you take the boundary $\partial F$ around the wire. Concerning the signs you just have to remember that the relative orientation of the boundary and the surface should be chosen by the right-hand rule.

Then you should think about the question, why you need a force to pull the circuit also the magnetic field doesn't do work on the charges.

 

[Simon Bridge]

My issue is that I have been thinking of the force produced by the magnetic field as something similar to the normal force in mechanics. Both only affect the way the object's path, but do no work. So it's confusing to me how the magnetic force can push charges around a wire.

... well, the normal force (say, from the surface of a ramp) does not push the objects around either, it does no work. The work done pushing something up a ramp is done by the person (or whatever) doing the pushing.

Of course, looking at a ramp, you can intuitively feel how the ramp forces the motion - there's a physical contact between object and ramp. With electromagnetism, you just have this force that seems to come out of nothing. However, your intuition about the ramp is incorrect: the "contact" in question is the same electromagnetism.

If you imagined a charged block constrained to move on a rail, and the rail slides through a magnetic field ... would that help?

Vanhees71 has good focussing questions for you.
Don't worry that nobody is just telling you the answer - this is something that everyone has to wrestle with to some extent and you get more out of it the more you can do for yourself. So, mostly. we are just focussing on your reasoning process.