How do you calculate a thickness dependant impedance to a so

[rwooduk]

... sound wave?

I need a simple method to calculate the impedance between water and silicone as ultrasound passes through them i.e. how much of the signal is reflected at the water silicone boundary.

The problem is I am having trouble finding the required equations, Wiki is extremely complicated (https://en.wikipedia.org/wiki/Acoustic_impedance) and other sites give an equation that doesn't include the thickness of the material (how is this possible? - please see image at end of this):

$I_{reflected} = I_{original} \frac{(Z_{1}-Z_{2})^{2}}{(Z_{1}+Z_{2})^{2}}$

My set up will be like this:

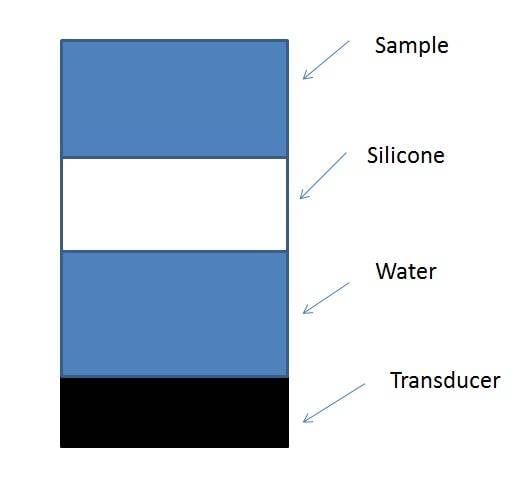
The idea of the silicone is to stop the sample from harming the transducer, also the silicone can't be in contact with the transducer as this could also cause harm to it. But I want as little as possible impedance from the silicone so I need to know how to calculate a thickness dependent impedance.

Can anyone suggest an equation that would be suited?

Thanks for any help on this.

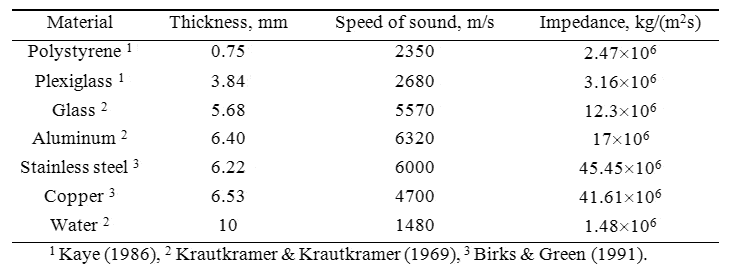
Table showing thickness dependence of the material:

 

[PWiz]

to calculate the impedance between water and silicone as ultrasound passes through them

Specific acoustic impedance is defined for a particular medium, not between mediums.

Ireflected=Ioriginal(Z1−Z2)2(Z1+Z2)2

Btw, this equation only works if sound is incident normally on a medium boundary. (This appears to be the case here.)

I think you can simply use $Z=\rho c$ to calculate the specific acoustic impedance for any medium ($\rho$ is the density of the medium and $c$ is the speed of sound in that medium), and then use the formula you posted to get your answer.

 

[rwooduk]

Many thanks for the reply.

Specific acoustic impedance is defined for a particular medium, not between mediums.

Thanks, I see, so the impedance of a material determines the degree to which the sound wave is attenuated? Wouldn't there be an impedance at the boundary between materials, hence why it can provide a measure of reflected and transmitted wave?

Btw, this equation only works if sound is incident normally on a medium boundary. (This appears to be the case here.)

I think you can simply use $Z=\rho c$ to calculate the specific acoustic impedance for any medium ($\rho$ is the density of the medium and $c$ is the speed of sound in that medium), and then use the formula you posted to get your answer.

How would thickness of the material be factored into the equation?

 

[PWiz]

How would thickness of the material be factored into the equation?

It doesn't come into the equation. The specific acoustic impedance is a property of a medium. The thickness of the medium has no effect on its value. Perhaps you want to know about the attenuation of ultrasound within a particular medium? If so, you can (approximately) model its behavior: $I = I_0 e^{-k x}$, where $I_0$ is the incident intensity, $k$ is the linear attenuation coefficient and $x$ is the thickness of the medium through which the ultrasound passes.

Wouldn't there be an impedance at the boundary between materials, hence why it can provide a measure of reflected and transmitted wave?

No. It's the difference between the specific acoustic impedance of the two media that determines the fraction of intensity that gets reflected.

so the impedance of a material determines the degree to which the sound wave is attenuated

Sort of. The density of the medium has an impact on the linear attenuation coefficient of the medium for ultrasound of any particular frequency.

 

[rwooduk]

It doesn't come into the equation. The specific acoustic impedance is a property of a medium. The thickness of the medium has no effect on its value. Perhaps you want to know about the attenuation of ultrasound within a particular medium? If so, you can (approximately) model its behavior: $I = I_0 e^{-k x}$, where $I_0$ is the incident intensity, $k$ is the linear attenuation coefficient and $x$ is the thickness of the medium through which the ultrasound passes.

No. It's the difference between the specific acoustic impedance of the two media that determines the fraction of intensity that gets reflected.

Sort of. The density of the medium has an impact on the linear attenuation coefficient of the medium for ultrasound of any particular frequency.

Ahh I've got it! Thats really helpful! Many thanks!