dect117
- 25
- 1
1. Homework Statement :
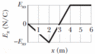
A graph of the x component of the electric field as a function of x in a region of space is shown in the figure [attached] below. The scale of the vertical axis is set by Exs = 47.5 N/C. The y and z components of the electric field are zero in this region. Suppose that the electric potential at the origin is 14 V.
V_f-V_i=-\int_{i}^{f} \vec E \cdot d \vec s
For part (a), I began by substituting in the appropriate values.
$$V_f-14=-\int_{0}^{2} E~d x$$
After integrating, I got
$$V_f-14=-E\left( 2 \right)$$
Finally, I substituted -47.5 in for E and solved for Vf.
$$V_f=47.5\left( 2 \right)+14=109$$
The answer I got was incorrect, though, and I can't see where I went wrong. I haven't really attempted parts (b) or (c) yet.
A graph of the x component of the electric field as a function of x in a region of space is shown in the figure [attached] below. The scale of the vertical axis is set by Exs = 47.5 N/C. The y and z components of the electric field are zero in this region. Suppose that the electric potential at the origin is 14 V.
(a) What is the electric potential at x = 2.0 m
(b) What is the greatest positive value of the electric potential for points on the x axis for which
0 ≤ x ≤ 6.0 m?
(c) For what value of x is the electric potential zero?
(b) What is the greatest positive value of the electric potential for points on the x axis for which
0 ≤ x ≤ 6.0 m?
(c) For what value of x is the electric potential zero?
Homework Equations
:[/B]V_f-V_i=-\int_{i}^{f} \vec E \cdot d \vec s
The Attempt at a Solution
:[/B]For part (a), I began by substituting in the appropriate values.
$$V_f-14=-\int_{0}^{2} E~d x$$
After integrating, I got
$$V_f-14=-E\left( 2 \right)$$
Finally, I substituted -47.5 in for E and solved for Vf.
$$V_f=47.5\left( 2 \right)+14=109$$
The answer I got was incorrect, though, and I can't see where I went wrong. I haven't really attempted parts (b) or (c) yet.