Kurtis McIntosh
- 6
- 0
Homework Statement
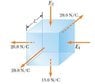
Assume the magnitude of the electric field on each face of the cube of edge L = 1.07 m in the figure below is uniform and the directions of the fields on each face are as indicated. (Take E1 = 35.1 N/C and E2 = 25.3 N/C.)
A.) Find the net electric flux through the cube.
B.) Find the net charge in the cube.
Homework Equations
Electric Flux = Electrical Field * Area
The Attempt at a Solution
I don't really understand how to solve for the net electric flux in the problem. I thought you would just take the difference in forces for each direction, multiplied by the area, then solve to find the magnitude using the x and y fluxes, but I'm clearly missing something here. I've included a photo of the cube. I've also tried solving for the flux on each individual face and then finding the sum of the fluxes, but that doesn't seem to work either.