SUMMARY
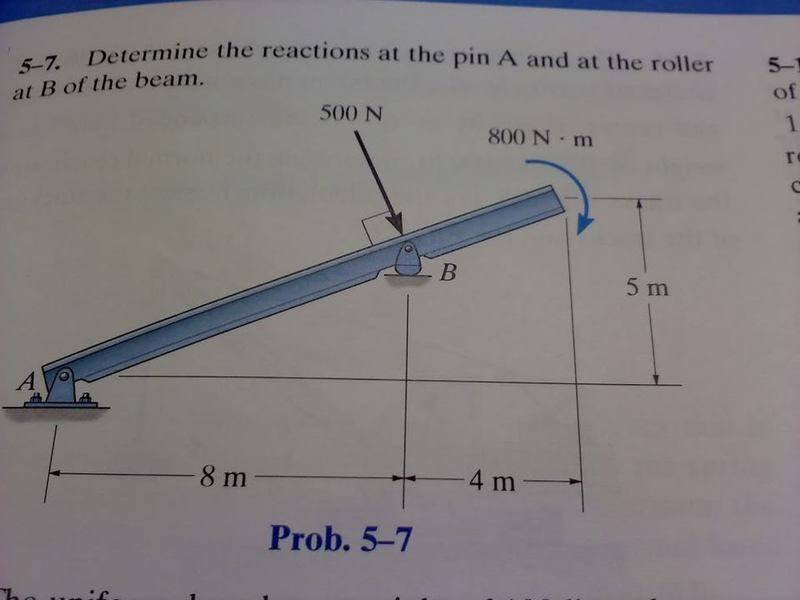
The discussion focuses on calculating the reactions at a pin support (A) and a roller support (B) on an inclined beam subjected to a vertical load. The calculated reactions are Ax = 192 N, Ay = 180 N, and By = 642 N. Key equations utilized include the equilibrium equations for forces and moments, specifically addressing the vertical and horizontal forces at the supports. The beam's inclination angle is 22 degrees, which affects the vertical force resolution of the applied load.
PREREQUISITES
- Understanding of static equilibrium principles
- Knowledge of reaction forces at supports (pin and roller)
- Familiarity with trigonometric functions for force resolution
- Ability to apply moment equations in structural analysis
NEXT STEPS
- Study the method of joints in static equilibrium
- Learn about the analysis of inclined beams in structural engineering
- Explore the application of trigonometry in resolving forces
- Review examples of calculating reactions in different support configurations
USEFUL FOR
This discussion is beneficial for civil engineers, structural analysts, and students studying mechanics of materials, particularly those focusing on beam analysis and support reactions.